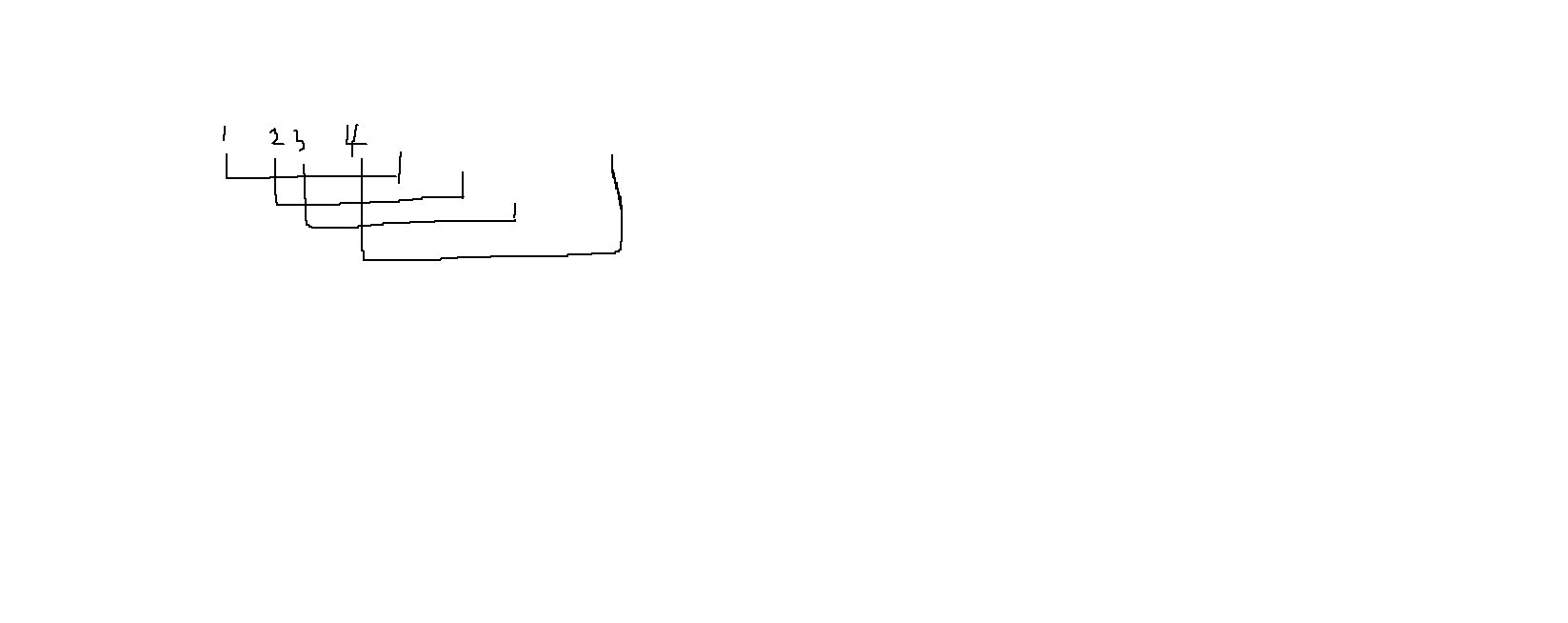做题记录1.0

一些零碎的做题记录。

CF1635D Infinite Set

题意

给定一个数组 $a$ 。构造一个集合 $S$ 。它里面的元素 $x$ 至少满足以下一条：

$x$ 在 $a$ 中；
$x=2y+1$ 且 $y$ 在 $S$ 中；
$x=4y$ 且 $y$ 在 $S$ 中。

给出 $p$ ，问 $S$ 中小于 $p$ 的元素有多少个，答案对 $10^9+7$ 取模。

数据范围： $1\leq n,p\leq 2\times 10^5,1\leq a_i\leq 10^9$ 。

题解

容易想到把各个数写成二进制表示，题目要问的就是 $S$ 中二进制下小于 $p$ 位的数有多少个。

先考虑由一个数能生成哪些数。不难发现，操作二就是在该数后面添一个 $1$ ，操作三就是在该数后面添两个 $0$ 。那么，如果这个数还有 $k$ 位可以填写，我们记恰好填 $k$ 位生成的数的个数为 $f_k$ 。则 $f_k=f_{k-1}+f_{k-2},f_0=f_1=1$ 。（转移方程可以考虑最后一次是填一个 $1$ 还是两个 $0$ ）所以总的贡献就是 $\sum\limits_{i=0}^kf_i$ 。

但是，初始给定的 $a$ 中可能有一些数可以通过其它数生成，需要把它们去掉。如果考虑一个数能生成哪些数，时间复杂度不对。我们可以反过来，考虑一个数可以被哪些数生成，这样的数级别是 $O(\log n)$ 的（因为只能是根据它的当前位，删去一个 $1$ 或是两个 $0$ 。）于是，我们可以维护一个关键数的集合。将数组 $a$ 排序，从小到大依次考察能够生成它的数是否在集合内，若不在，则计算它的贡献并将它加入。

代码

#include <bits/stdc++.h>
using namespace std;
const int maxn=2e5+5;
const int p=1e9+7;
int a[maxn],f[maxn];
void init()
{
    f[0]=1,f[1]=1;
    for(int i=2;i<maxn;i++) f[i]=(f[i-1]+f[i-2])%p;
    for(int i=1;i<maxn;i++) f[i]=(f[i]+f[i-1])%p;
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    init();
    int n,m;cin>>n>>m;
    int ans=0;
    set<int> s;
    for(int i=1;i<=n;i++) cin>>a[i];
    sort(a+1,a+n+1);
    for(int i=1;i<=n;i++)
    {
        int b=a[i],c=a[i],cnt=0;
        vector<int> v;
        while(b)
        {
            v.push_back(b&1);
            b>>=1;
            cnt++;
        }
        int k=(int)v.size();
        bool ok=1;
        for(int i=0;i<k;i++)
        {
            if(s.find(c)!=s.end()) ok=0;
            if(v[i]) c>>=1;
            else 
            {
                if(!v[i+1]) 
                {
                    c>>=2;
                    i++;
                }
                else break;
            }
        }
        if(ok&&m>=k) 
        {
            s.insert(a[i]);
            ans=(ans+f[m-k])%p;
        }
    }
    cout<<ans<<'\n';
    return 0;
}

CF1634D Finding Zero

题意

给定一个长度为 $n$ 的数组 $a$ ，当中恰好有一个元素为 $0$ 。每次询问选择三个互不相同的 $i,j,k$ ，返回 $\max(a_i,a_j,a_k)-\min(a_i,a_j,a_k)$ 。要求在 $2n-2$ 次询问内，确定 $0$ 可能在哪两个元素中。

题解

考虑用两次操作排除掉一个合法的元素。事实上，可以一次考虑四个元素 $a,b,c,d$ ，用四次询问排除掉两个元素。如果有一个元素为 $0$ ，那么带有它的询问结果一定不会是四个中前两大的。（有至少两次询问的结果都是最大值减去 $0$ ，而该询问是最大值减去一个正数）

代码

#include <bits/stdc++.h>
 
#define all(x) (x).begin(), (x).end()
#define len(x) (int) (x).size()
 
using namespace std;
 
 
int get(const vector <int>& x) {
    cout << "? " << x[0] + 1 << " " << x[1] + 1 << " " << x[2] + 1 << endl;
    int ans;
    cin >> ans;
    return ans;
}
 
 
signed main() {
    ios_base::sync_with_stdio();
    cin.tie(nullptr);
    
    int t;
    cin >> t;
    
    while(t --> 0) {
        int n;
        cin >> n;
    
        pair <int, int> possible = {0, 1};
        for (int i = 2; i < n - 1; i += 2) {
            vector <pair <int, int>> ch(4);
            vector <int> now = {possible.first, possible.second, i, i + 1};
            for (int j = 0; j < 4; j++) {
                vector <int> x = now;
                x.erase(x.begin() + j);
                ch[j] = {get(x), now[j]};
            }
            sort(all(ch));
            possible = {ch[0].second, ch[1].second};
        }
        if (n % 2 == 1) {
            int other = 0;
            while (possible.first == other || possible.second == other) {
                other++;
            }
            vector <pair <int, int>> ch(4);
            vector <int> now = {possible.first, possible.second, n - 1, other};
            for (int j = 0; j < 4; j++) {
                vector <int> x = now;
                x.erase(x.begin() + j);
                ch[j] = {get(x), now[j]};
            }
            sort(all(ch));
            possible = {ch[0].second, ch[1].second};
        }
        cout << "! " << possible.first + 1 << " " << possible.second + 1 << endl;
    }
 
    return 0;
}

CF1630C Paint the Middle

题意

给出一个长度为 $n$ 的数组 $a$ 。每次可以选择 $i<j<k$ 且 $a_i=a_k$ ，将 $a_j$ 删除。问最多能删除多少个元素。

数据范围： $3\leq n\leq 2\times 10^5,1\leq a_i\leq n$ 。

题解

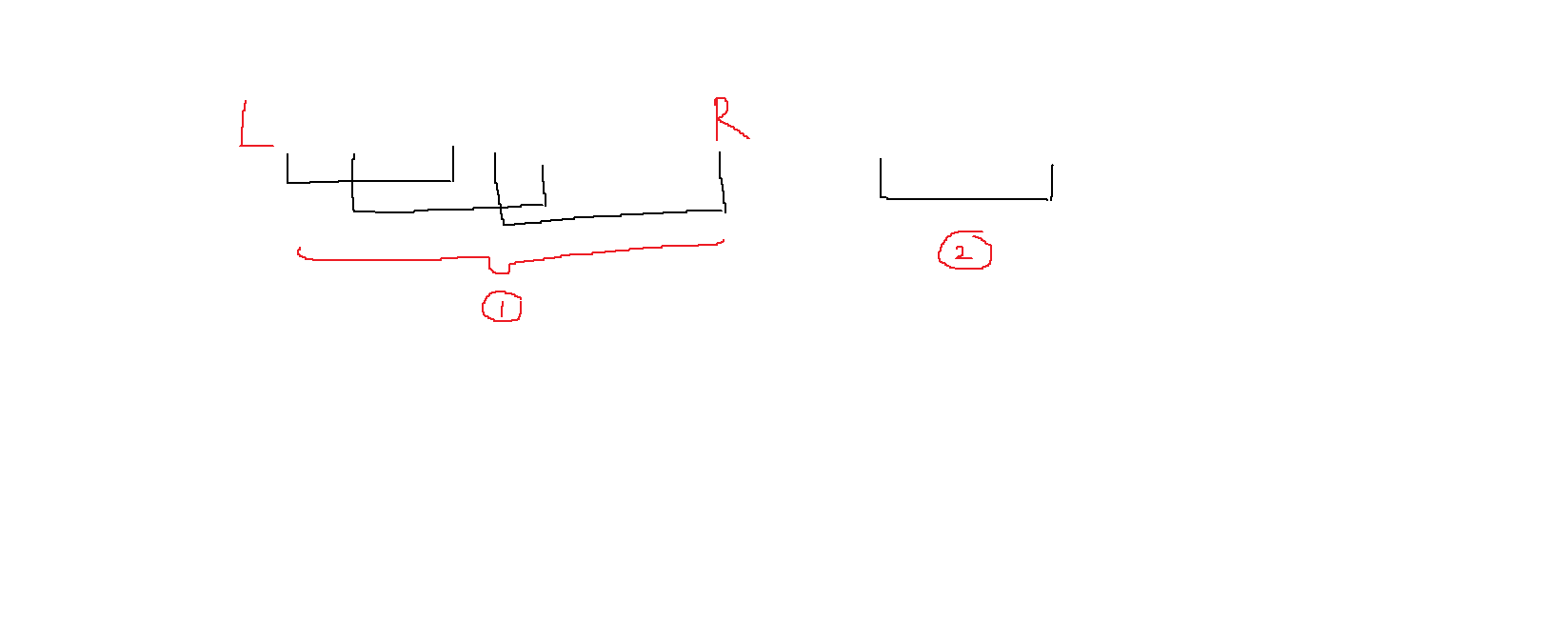
对于每种颜色，我们只关心它第一次出现和最后一次出现。这样，每种颜色可以用一条线段 $(l,r)$ 来代表。显然，对于被包含的线段，它们是不需要考虑的，先将它们剔除。

接下来处理区间相交的情况。我们可以将线段分成若干不交的大区间，如下图所示。我们逐个区间进行考虑。

首先考虑两条线段相交，那么非端点的部分可以直接删除，此外，我们还可以删除中间的某一个端点。这启发我们，是否可以利用后一条线段将前一条线段的右端点删除呢？但这还不够优秀。事实上，我们需要找到最少的线段数覆盖整个区间。这时，其余的所有线段两端都可以被删除，这是最优的情况。如下图所示，此时选择1和4是最优的，2和3的两个端点都可以被删除。

这样这题就做完了。

代码

#include <bits/stdc++.h>
using namespace std;
const int maxn=2e5+5;
int m,tmp,a[maxn],l[maxn],r[maxn];
struct node
{
    int l,r;
    bool operator < (const node &x) {return l==x.l?r<x.r:l<x.l;}
}b[maxn],c[maxn];
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int n;cin>>n;
    for(int i=1;i<=n;i++) cin>>a[i];
    for(int i=1;i<=n;i++)
    {
        if(!l[a[i]]) l[a[i]]=i;
        r[a[i]]=i;
    }
    for(int i=1;i<=n;i++)
        if(l[a[i]]&&r[a[i]]>l[a[i]]) b[++tmp]={l[a[i]],r[a[i]]};
    sort(b+1,b+tmp+1);
    for(int i=1;i<=tmp;i++)
    {
        int nxt=i+1;
        while(nxt<=tmp&&b[nxt].r<=b[i].r) nxt++;
        c[++m]=b[i];
        i=nxt-1;
    }
    int ans=0;
    for(int i=1;i<=m;i++)
    {
        int nxt=i+1,L=c[i].l,R=c[i].r,cnt=1;
        while(nxt<=m&&c[nxt].l<R) 
        {
           while(nxt<=m&&c[nxt].l<R) nxt++;
           R=c[nxt-1].r,cnt++;
        }
        ans+=R-L-cnt;
        i=nxt-1;
    }
    cout<<ans<<'\n';
    return 0;
}

CF1630B Range and Partition

题意

给出一个长度为 $n$ 的数组 $a$ 。给定一个区间 $[x,y]$ ，将数组分为 $k$ 个连续的子段，要求每个子段中落在区间 $[x,y]$ 内的数严格大于落在区间外的。试最小化 $y-x$ 。

数据范围： $1\leq k\leq n\leq 2\times 10^5,1\leq a_i\leq n$ 。

题解

记 $a$ 中落在区间 $[x,y]$ 内的数为 $x$ ，当 $x-(n-x)\geq k$ 时，一定有解。方案时每当落在区间内的数大于落在区间外的就断开，最后剩下的一段中落在区间内的数一定也大于落在区间外的数。

那么问题就转变成了最小化区间长度，使得落在区间内的数大于某个值。这是个经典问题，可以用滑动窗口解决。

代码

#include <bits/stdc++.h>
using namespace std;
const int maxn=2e5+5;
int a[maxn],b[maxn];
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int t;cin>>t;
    while(t--)
    {
        int n,k;cin>>n>>k;
        for(int i=1;i<=n;i++) b[i]=0;
        for(int i=1;i<=n;i++) cin>>a[i],b[a[i]]++;
        int ans=0x3f3f3f3f,l=0,r=0,j=0,cnt=0;
        for(int i=1;i<=n;i++)
        {       
            while(2*cnt<n+k&&j<n)
            {
                j++;
                cnt+=b[j];
            }
            if(2*cnt>=n+k&&j-i<ans) ans=j-i,l=i,r=j;
            cnt-=b[i];
        }
        cout<<l<<' '<<r<<'\n';
        for(int i=1;i<=n;i++)
        {
            int res=0;
            vector<int> v;
            if(k>1)
            {
                for(int j=i;;j++)
                {   
                    if(a[j]>=l&&a[j]<=r) res++;
                    else res--;
                    v.push_back(j);
                    if(res==1)
                    {
                        cout<<v.front()<<' '<<v.back()<<'\n';
                        k--;
                        i=j;
                        break;
                    }
                }
            }
            else
            {
                cout<<i<<' '<<n<<'\n';
                break;
            }
        }
    }
    return 0;
}

CF1628D Game on Sum

题意

Alice和Bob在玩一个游戏。每次操作Alice给出一个 $0\sim k$ 之间的实数，Bob选择将令总和加上或减去它。一共进行 $n$ 轮，Bob至少要进行 $m$ 次加操作。Alice希望最大化总和，Bob希望最小化总和。求两人最优操作下总和的值。答案对 $10^9+7$ 取模。

数据范围：

easy version： $1\leq m\leq n\leq 2000,0\leq k<10^9+7$ 。

hard version： $1\leq m\leq n\leq 10^6,0\leq k<10^9+7$ 。

题解

先考虑easy version：

记 $f_{i,j}$ 为剩余 $i$ 次加法 $j$ 次减法时的总和。记当前这轮Alice选择的数为 $x$ ，则 $f_{i,j}=\min(f_{i-1},j+x,f_{i,j-1}-x)$ 。显然，两项相等时 $f_{i,j}$ 最大。所以，有转移方程 $f_{i,j}=\dfrac{f_{i-1,j}+f_{i,j-1}}{2}$ 。直接转移，时间复杂度为 $O(n^2)$ 。

然后考虑优化：

我们去考虑每个 $f_{i,0}$ 对于最终答案的贡献。我们发现它的贡献就是在网格中它走到 $(m,n-m)$ 的方案数除以 $2$ 的路径长度次方。预处理一下，时间复杂度为 $O(n)$ 。不过我的状态设计可能有点问题，所以 $n=m$ 的情况需要特判。

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=1e6;
const int p=1e9+7;
const int inv2=500000004;
ll fac[maxn+5],ifac[maxn+5],P2[maxn+5];
ll fpow(ll a,ll b)
{
    ll res=1;
    while(b)
    {
        if(b&1) res=res*a%p;
        a=a*a%p;
        b>>=1;
    }
    return res;
}
void init()
{
    fac[0]=1;
    for(int i=1;i<=maxn;i++) fac[i]=i*fac[i-1]%p;
    ifac[maxn]=fpow(fac[maxn],p-2);
    for(int i=maxn;i;i--) ifac[i-1]=i*ifac[i]%p;
    P2[0]=1;
    for(int i=1;i<=maxn;i++) P2[i]=P2[i-1]*inv2%p;
}
ll C(ll n,ll m)
{
    return fac[n]*ifac[n-m]%p*ifac[m]%p;
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    init();
    int t;cin>>t;
    while(t--)
    {
        ll n,m,k;cin>>n>>m>>k;
        if(n==m)
        {
            cout<<n*k%p<<'\n';
            continue;
        }
        ll ans=0;
        for(int i=1;i<=m;i++) ans=(ans+i*k%p*C(n-i-1,m-i)%p*P2[n-i]%p)%p;
        cout<<ans<<'\n';
    }
    return 0;
}

ABC301E Pac-Takahashi

题意

给出一个 $H$ 行 $W$ 列的网格。每个格子是以下五种中的一种：

S 代表起点位置
G 代表终点位置
. 代表空白位置
# 代表障碍位置
o 代表糖果位置

（保证糖果的数量不超过 $18$ 个）

要求在 $T$ 步内从起点走到终点，求在此基础上可以吃到的糖果的最大数量。

题解

将起点、终点、糖果都当作关键点，预处理出关键点两两之间的距离 $d_{i,j}$ 。考虑状压dp：记 $f_{i,S}$ 表示最后到达关键点 $i$ ，已走过的关键点集合为 $S$ 所需要的最小步数。则 $f_{i,S\cup j}\leftarrow f_{i,S}+d_{i,j}$ 。

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
int h,w,t,cnt,sx,sy,gx,gy;
int dx[]={0,1,0,-1},dy[]={1,0,-1,0};
char a[305][305];
int dis[305][305],d[25][25];
bool vis[305][305];
ll f[25][(1<<20)+5];
pii candy[25];
bool inside(int x,int y) {return x>=1&&x<=h&&y>=1&&y<=w;}
void bfs(int i,int x,int y)
{
    memset(vis,0,sizeof(vis));
    memset(dis,0x3f,sizeof(dis));
    queue<pii> q;
    q.push({x,y});dis[x][y]=0;vis[x][y]=1;
    while(!q.empty())
    {
        int xx=q.front().first,yy=q.front().second;q.pop();
        for(int k=0;k<4;k++)
        {
            int tx=xx+dx[k],ty=yy+dy[k];
            if(!inside(tx,ty)||a[tx][ty]=='#'||vis[tx][ty]) continue;
            q.push({tx,ty});
            vis[tx][ty]=1;
            dis[tx][ty]=dis[xx][yy]+1;
        }
    }
    for(int j=0;j<=cnt;j++) d[i][j]=dis[candy[j].first][candy[j].second];
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cin>>h>>w>>t;
    for(int i=1;i<=h;i++)
        for(int j=1;j<=w;j++) 
        {
            cin>>a[i][j];
            if(a[i][j]=='o') candy[++cnt]={i,j};
            if(a[i][j]=='S') sx=i,sy=j;
            if(a[i][j]=='G') gx=i,gy=j;
        }
    candy[0]={sx,sy},candy[++cnt]={gx,gy};
    for(int i=0;i<=cnt;i++) bfs(i,candy[i].first,candy[i].second);
    for(int i=0;i<=cnt;i++)
        for(int j=0;j<=cnt;j++) cout<<d[i][j]<<" \n"[j==cnt];
    memset(f,0x3f,sizeof(f));
    f[0][1]=0;
    for(int s=0;s<(1<<(cnt+1));s++)
        for(int i=0;i<=cnt;i++)
        {
            if(!(s>>i&1)) continue; 
            for(int j=0;j<=cnt;j++)
            {
                f[j][s|(1<<j)]=min(f[j][s|(1<<j)],f[i][s]+d[i][j]);
            }
        }
    int ans=1;
    for(int s=0;s<(1<<(cnt+1));s++) 
            if(f[cnt][s]<=t) ans=max(ans,__builtin_popcount(s));
    cout<<ans-2<<'\n';
    return 0;
}

ABC301F Anti-DDoS

题意

一个DDoS串定义如下：

由四个字母组成
第一个，第二个和第四个字母为大写，第三个为小写
第一个字母和第二个字母相同

给出一个串 $S$ ，有一些位置为 ?，可以任意填入大写字母或小写字母。求最终得到的不含有子序列为 DDoS 串的不同的 $S$ 的数量。

题解

将 DDoS 拆分：设 $f_{i,0/1/2}$ 表示前 $i$ 个字符不出现 DD/DDo/DDoS 的方案数。则答案为 $f_{n,2}$ 。

$f_{i,0}$ ：我们维护是否出现过两个相同的大写字母，未出现过的大写字母个数 $k$ ，问号个数 $m$ 。若已经出现过两个相同的大写字母，则 $f_{i,0}=0$ 。否则，我们枚举问号上填写的大写字母，并分配给各个问号，其余问号可以填写任意小写字母。得到方程： $f_{i,0}=\sum\limits_{j=0}^{\min(k,m)}\binom{m}{j}\times \binom{n}{j}\times j!\times 26^{m-j}$ 。

$f_{i,1}$ ：若该位置为大写字母，那么只要前面的位置不出现DDo即可， $f_{i,1}=f_{i-1,1}$ 。若该位置为小写字母，那么前面的位置不能出现DD， $f_{i,1}=f_{i-1,0}$ 。若该位置为问号，则 $f_{i,1}=26\times f_{i-1,0}+26\times f_{i-1,1}$ 。

$f_{i,2}$ 的转移与 $f_{i,1}$ 类似。

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=3e5+5;
const int p=998244353;
bool vis[26];
char s[maxn];
ll f[maxn][3],fac[maxn],ifac[maxn];
ll fpow(ll a,ll b)
{
    ll res=1;
    while(b)
    {
        if(b&1)res=res*a%p;
        a=a*a%p;
        b>>=1;
    }
    return res;
}
void init()
{
    fac[0]=1;
    for(int i=1;i<maxn;i++) fac[i]=i*fac[i-1]%p;
    ifac[maxn-1]=fpow(fac[maxn-1],p-2);
    for(int i=maxn-1;i;i--) ifac[i-1]=i*ifac[i]%p;
}
ll C(ll n,ll m) 
{
    if(n<m) return 0;
    return fac[n]*ifac[m]%p*ifac[n-m]%p;
}
ll solve(int k,int m)
{
    ll res=0;
    for(int j=0;j<=min(m,k);j++) res=(res+C(m,j)*C(k,j)%p*fac[j]%p*fpow(26,m-j)%p)%p;
    return res;
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    init();
    cin>>(s+1);
    int n=strlen(s+1);
    bool flag=1;
    int k=26,m=0;
    f[0][0]=f[0][1]=f[0][2]=1;
    for(int i=1;i<=n;i++)
    {
        if('A'<=s[i]&&s[i]<='Z') 
        {
            int p=s[i]-'A';
            if(vis[p]) flag=0;
            else
            {
                vis[p]=1;
                k--;
            }
            f[i][0]=flag?solve(k,m):0;
            f[i][1]=f[i-1][1];
            f[i][2]=f[i-1][1];
        }
        else if('a'<=s[i]&&s[i]<='z')
        {
            f[i][0]=flag?solve(k,m):0;
            f[i][1]=f[i-1][0];
            f[i][2]=f[i-1][2];
        }
        else
        {
            m++;
            f[i][0]=flag?solve(k,m):0;
            f[i][1]=26*(f[i-1][0]+f[i-1][1])%p;
            f[i][2]=26*(f[i-1][1]+f[i-1][2])%p;
        }
    }
    cout<<f[n][2]<<'\n';
    return 0;
}

ABC300F More Holidays

题意

给出一个长度为 $n$ 的字符串 $S$ ，只含有字符 o 和 x。令 $T$ 为 $m$ 个字符串 $S$ 的拼接，可以其中的将 $k$ 个 x 修改为 o。求能得到仅含 o 的最长连续子串的长度最大值。

题解

不难发现，最终得到的结果一定是后缀+连续的S+前缀的形式。首先容易计算至多可以将多少个S修改为全 o。剩下的修改次数则用来修改前一个串的后缀和后一个串的前缀。为了计算，我们将两个S拼接起来，求出可能的答案。这个问题可以用双指针解决：固定左端点，右端点显然是单调不降的，保证区间内的 x 个数不超过剩下修改次数即可。

需要注意的是，将部分S修改为全o后，剩下的串可能只有一个，此时需要避免计算跨越两个S的答案。若所有串都被修改，直接输出结果。

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=3e5+5;
char s[2*maxn];
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    ll n,m,k;cin>>n>>m>>k;
    cin>>(s+1);
    for(int i=1;i<=n;i++) s[i+n]=s[i];
    ll x=0;
    for(int i=1;i<=n;i++)
        if(s[i]=='x') x++;
    ll cnt=k/x;
    ll mx=0,cur=(s[1]=='x'),res=k%x;
    for(ll l=1,r=1;l<=n;l++)
    {
        while(r+1<=2*n&&cur+(s[r+1]=='x')<=res) cur+=(s[++r]=='x');
        if(m-cnt==1) mx=max(mx,min(r,n)-l+1);
        else if(m-cnt>1) mx=max(mx,r-l+1);
        cur-=(s[l]=='x');
    }
    cout<<n*cnt+mx<<'\n';
    return 0;
}

ABC300G P-smooth number

题意

给定 $n$ ，求不超过 $n$ 的最大质因子不超过 $P$ 的数的个数。

数据范围： $1\leq n\leq 10^{16},2\leq P\leq 100$ 。

题解

题目很贴心的给了这样一组数据：

1 2	`10000000000000000 97 2345134674`

这已经是极限情况了，最终的数也不是很多。所以我们可以很快得到一个乱搞的做法：反过来爆搜，最后处理到 $2$ 时答案就是 $\lfloor \log_2 res\rfloor$ 。对于 $n$ 比较小的，再记忆化一下。其实这样已经可以通过了，甚至跑得飞快。

还有一个相对靠谱一些的做法：折半搜索。我们考虑搜出质因子仅含 $2,3,5,7,11,13,17$ 的不超过 $n$ 的数放在第一个集合内，质因子大于 $17$ 的放在第二个集合内。然后枚举第一个集合内的数，在第二个集合内二分查找。

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int cnt,pri[105];
bool vis[105];
ll n,p;
vector<ll> v1,v2;
void init(int n)
{
    for(int i=2;i<=n;i++)
    {
        if(!vis[i]) pri[++cnt]=i;
        for(int j=1;j<=cnt&&i*pri[j]<=n;j++)
        {
            vis[i*pri[j]]=1;
            if(i%pri[j]==0) break;
        }
    }
}
void dfs1(int cur,int limit,ll sum)
{
    if(cur==limit+1)
    {
        v1.push_back(sum);
        return;
    }
    for(ll res=1;sum*res<=n;res*=pri[cur]) dfs1(cur+1,limit,sum*res);
}
void dfs2(int cur,int limit,ll sum)
{
    if(cur==limit+1)
    {
        v2.push_back(sum);
        return;
    }
    for(ll res=1;sum*res<=n;res*=pri[cur]) dfs2(cur+1,limit,sum*res);    
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cin>>n>>p;
    init(p);
    dfs1(1,min(7,cnt),1);
    if(cnt>=8) dfs2(8,cnt,1);
    sort(v1.begin(),v1.end()),sort(v2.begin(),v2.end());
    //cout<<v1.size()<<' '<<v2.size()<<'\n';
    if(v2.empty()) cout<<v1.size()<<'\n';
    else
    {
        ll ans=0;
        for(auto i:v1) ans+=upper_bound(v2.begin(),v2.end(),n/i)-v2.begin();
        cout<<ans<<'\n';
    }
    return 0;
}

ABC285E Work or Rest

题意

一周有 $n$ 天，每天可以有两种安排：

休息，不获得收益
工作，收益为 $A_{\min(x,y)}$ ，其中 $x$ 和 $y$ 分别为该天之前最近的休息日和该天之后最近的休息日（可能在下周）。

一周至少休息一天。要求最大的收益。

题解

一道经典的问题。由于下一周的第一个休息日可能会对上一周产生影响，不太好处理。所以，我们钦定每周的第一天必定休息，这并不会影响答案，因为一周一周是循环的。

令 $f_i$ 表示前 $i$ 天，第 $i$ 天休息能得到的最大收益。则

f_i=\max_{j=1}^{j<i} f_j+\omega(i-j-1)

这里的转移是在枚举前一个休息的日子， $\omega(i-j-1)$ 表示在两个休息日间一段连续的工作日所能得到的收益，可以预处理前缀和快速计算。

最终的答案为 $\max\limits_{i=1}^nf_i+\omega(n-i)$ 。

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int a[5005];
ll sum[5005],f[5005];
ll cal(int x)
{
    if(x&1) return 2*sum[x/2]+a[x/2+1];
    else return 2*sum[x/2];
}   
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int n;cin>>n;
    for(int i=1;i<=n;i++) cin>>a[i],sum[i]=sum[i-1]+a[i];
    for(int i=2;i<=n;i++) 
        for(int j=1;j<=i-1;j++) f[i]=max(f[i],f[j]+cal(i-j-1));
    ll ans=0;
    for(int i=1;i<=n;i++) ans=max(ans,f[i]+cal(n-i));
    cout<<ans<<'\n';
    return 0;
}

ABC284G Only Once

题意

给定一个长度为 $n$ 的数组 $a$ ， $1\leq a_i\leq n$ 。定义数组 $b_i=(b_{i,1},b_{i,2},\cdots,b_{i,10^{100}})$ 为

$b_{i,1}=i$
$b_{i,j+1}=a_{b_{i,j}}$

定义 $S_i$ 为 $b_i$ 中只出现一次的数字个数。对于所有可能的 $a$ ，求出它们的 $\sum\limits_{i=1}^nS_i$ 之和。

题解

我们可以由 $i$ 向 $a_i$ 连边，不能发现会得到一个基环森林。每个点为起点时，它的贡献为它走入环之前的步数。比如考虑 $a=\{2,2,3,4\}$ ，可以画出这样一张图，容易得到 $b_1=2,b_2=1,b_3=b_4=0$ 。

由于对称性，我们只需要计算 $1$ 号点的贡献，然后乘上 $n$ 就行了。这时，我们只关心从 $1$ 号点出发走到环的路径上的点和环上的点，因为这些点的连边情况是确定的。记这些点为 $c_1\to c_2\to \cdots \to c_l$ ，设 $c_l\to c_p$ ，那么 $1$ 号点的贡献为 $p-1$ ，因为 $c_p$ 及后面的点都在环上。此时，方案数是容易求得的，我们固定了 $c_1$ 为 $1$ ，在剩下 $n-1$ 个数中选 $l-1$ 个分配个 $l-1$ 个点（排列），然后对于剩余的 $n-l$ 个点，它们可以任意连边。所以方案为

f(l)=A_{n-1}^{l-1}\times n^{n-l}\times \sum_{p=1}^l(p-1)=A_{n-1}^{l-1}\times n^{n-l}\times \frac{l\times (l-1)}{2}

最终的答案为

n\times \sum_{l=1}^n f(l)

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=2e5+5;
ll P[maxn];
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    ll n,m;cin>>n>>m;
    P[0]=1;
    for(int i=1;i<n;i++) P[i]=n*P[i-1]%m;
    ll ans=0,x=1;
    for(int i=1;i<=n;i++) 
    {
        ans=(ans+x*P[n-i]%m*(1ll*i*(i-1)/2%m)%m)%m;
        x=x*(n-i)%m;
    }
    cout<<ans*n%m<<'\n';
    return 0;
}

ABC283G Partial Xor Enumeration

题意

给定一个数组 $a$ ，记 $S$ 为从这些数组中任意选取一些数其异或值组成的集合，输出集合内排名为 $L\sim R$ 的数。

题解

线性基裸题，等有时间系统学习一下。

本题的注意点是由于选择的数可以是 $0$ 个，所以集合 $S$ 中一定存在 $0$ 。

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=2e5+5;
const int B=60;
bool zero;
int cnt;
ll a[maxn],base[65],p[65];
void insert(ll x)
{
    for(int i=B;i>=0;i--)
        if(x&(1ll<<i))
        {
            if(!base[i])
            {
                cnt++;
                base[i]=x;
                break;
            }
            else x^=base[i];
        }
}
ll qmn()
{
    if(zero) return 0;
    for(int i=0;i<=B;i++)
        if(base[i]) return base[i];
    return 0;
}
ll qmx()
{
    ll res=0;
    for(int i=B;i>=0;i--)
        if((res^base[i])>res) res^=base[i];
    return res;
}
void rebuild()
{
    cnt=0;
    for(int i=B;i>=0;i--)
        for(int j=i-1;j>=0;j--)
            if(base[i]&(1ll<<j)) base[i]^=base[j];
    for(int i=0;i<=B;i++) 
        if(base[i]) p[cnt++]=base[i];
}
ll qk(ll k)
{
    if(zero) 
    {
        if(k==1) return 0;
        else k--;
    }
    if(k>=(1ll<<cnt)) return -1;
    ll res=0;
    for(int i=B;i>=0;i--)
        if(k&(1ll<<i)) res^=p[i];
    return res;
}
ll rk(ll x)
{
    ll res=0;
    for(int i=cnt-1;i>=0;i--)
        if(x>=p[i]) res+=(1ll<<i),x^=p[i];
    return res+zero;
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int n;cin>>n;
    ll l,r;cin>>l>>r;
    for(int i=1;i<=n;i++) cin>>a[i],insert(a[i]);
    //zero=cnt!=n;
    zero=1;
    rebuild();
    for(ll i=l;i<=r;i++) cout<<qk(i)<<" \n"[i==r];
    return 0;
}

ABC282G Similar Permutation

题意

定义两个长度为 $n$ 的排列的相似度为符合下列条件的 $i$ 的个数：

$(A_{i+1}-A_i)(B_{i+1}-B_i)>0$

求有多少对长度为 $n$ 的排列 $A,B$ 满足相似度为 $K$ 。

题解

https://atcoder.jp/contests/dp/tasks/dp_t

感觉搞明白上面那道题这道题就做完了！

设 $f_{i,j,k,t}$ 表示前 $i$ 个位置， $A$ 中第 $i$ 个位置在前 $i$ 个里排名为 $j$ ， $B$ 为 $k$ ，相似度为 $t$ 的数量。

则转移方程为

f_{i,j,k,t}=\sum_{x=1}^{j-1}\sum_{y=1}^{k-1}f_{i-1,x,y,t-1}+\sum_{x=j}^{i-1}\sum_{y=k}^{i-1}f_{i-1,x,y,t-1}+\sum_{x=1}^{j-1}\sum_{y=k}^{i-1}f_{i-1,x,y,t}+\sum_{x=j}^{i-1}\sum_{y=1}^{k-1}f_{i-1,x,y,t}

利用二维前缀和优化一下就行了。

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=105;
int n,m,p;
ll f[N][N][N],sum[N][N][N];
ll query(int x1,int y1,int x2,int y2,int t)
{
    return (sum[x2][y2][t]-sum[x2][y1-1][t]-sum[x1-1][y2][t]+sum[x1-1][y1-1][t]+2*p)%p;
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cin>>n>>m>>p;
    f[1][1][0]=1;
    for(int i=2;i<=n;i++)
    {
        for(int j=1;j<i;j++)
            for(int k=1;k<i;k++)
                for(int t=0;t<i-1;t++)
                    sum[j][k][t]=(sum[j-1][k][t]+sum[j][k-1][t]-sum[j-1][k-1][t]+f[j][k][t]+p)%p;
        for(int j=1;j<=i;j++)
            for(int k=1;k<=i;k++)
                for(int t=0;t<i;t++)
                {
                    if(!t) f[j][k][t]=(query(1,k,j-1,i-1,t)+query(j,1,i-1,k-1,t))%p;
                    else f[j][k][t]=(query(1,1,j-1,k-1,t-1)+query(j,k,i-1,i-1,t-1)+query(1,k,j-1,i-1,t)+query(j,1,i-1,k-1,t))%p;
                }
    }
    ll ans=0;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++) ans=(ans+f[i][j][m])%p;
    cout<<ans<<'\n';
    return 0;
}

ABC299F Square Subsequence

题意

给出一个字符串 $S$ ，求 $S$ 中所有满足 $TT$ 为 $S$ 子序列的子串 $T$ 。

题解

我什么时候才能会dp啊！！！

考虑从 $TT$ 入手，记 $f_{i,j}$ 表示 $T$ 在 $[1,i]$ 和 $[i+1,j]$ 内都构成子序列，且 $s_i,s_j$ 必须选。那么如果 $s_i=s_j$ ，它可以由所有的 $\sum\limits_{x<i,y<j}f_{x,y}$ 转移而来（相当于是在原来的 $T$ 后面添加了一个相同的字符）。但是可能会出现重复的情况，所以我们钦定相同字符只添加最靠左的。即记 $nxt_{i,c}$ 表示 $i$ 后面字符 $c$ 第一次出现的位置，那么 $f_{i,j}$ 只向 $f_{nxt_{i,c},nxt_{j,c}}$ 转移。

具体的转移过程参考代码。

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=105;
const int inf=0x3f3f3f3f;
const int p=998244353;
char s[N];
int nxt[N][26];
ll f[N][N];
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cin>>(s+1);
    int n=strlen(s+1);
    for(int j=0;j<26;j++) nxt[n][j]=inf;
    for(int i=n-1;i>=0;i--)
    {
        for(int j=0;j<26;j++) nxt[i][j]=nxt[i+1][j];
        nxt[i][s[i+1]-'a']=i+1;
    }
    ll ans=0;
    for(int i=1;i<n;i++)
    {
        memset(f,0,sizeof(f));
        for(int j=0;j<26;j++)
            if(nxt[0][j]<=i&&nxt[i][j]<=n) f[nxt[0][j]][nxt[i][j]]++;
        for(int j=1;j<=i;j++)
            for(int k=i+1;k<=n;k++)
                if(s[j]==s[k])
                {
                    for(int c=0;c<26;c++)
                        if(nxt[j][c]<=i&&nxt[k][c]<=n) f[nxt[j][c]][nxt[k][c]]=(f[nxt[j][c]][nxt[k][c]]+f[j][k])%p;
                }
        for(int j=i+1;j<=n;j++) ans=(ans+f[i][j])%p;
    }
    cout<<ans<<'\n';
    return 0;
}

ABC275E Sugoroku 4

题意

从 $0$ 号格子出发到 $n$ 号格子，每次走等于骰子点数的步数，如果超过了 $n$ ，则需要掉头走完多余的步数，求 $k$ 次内走到 $n$ 号格子的概率。

题解

很傻逼的一道题目，但是我更傻逼。不仅思路想错了，写的时候也是一堆问题。

设 $f_{i,j}$ 为到达第 $i$ 号格子走了 $j$ 步的概率，很容易得到转移方程

f_{i,j}=\sum_{t=\max(i-m,0)}^{i-1}\frac{1}{m}f_{t,j-1}+\sum_{t=2n-m-i}^{n-1}\frac{1}{m}f_{t,j-1}[i\neq n]

（ $i=n$ 时第二项和第一项一样，会算重复。）

这个方程显然是没有后效性的，因为 $j$ 不同。当时不知道怎么想的，以为它有后效性，还想着用高斯消元做…

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1005;
const int p=998244353;
ll f[N][N];
ll fpow(ll a,ll b)
{
    ll res=1;
    while(b)
    {
        if(b&1) res=res*a%p;
        a=a*a%p;
        b>>=1;
    }
    return res;
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int n,m,k;cin>>n>>m>>k;
    ll inv=fpow(m,p-2);
    f[0][0]=1;
    for(int j=1;j<=k;j++) 
        for(int i=1;i<=n;i++)
        {
            for(int t=max(0,i-m);t<=i-1;t++) f[i][j]=(f[i][j]+inv*f[t][j-1])%p;
            if(i!=n) for(int t=2*n-m-i;t<=n-1;t++) f[i][j]=(f[i][j]+inv*f[t][j-1])%p;
        }
    ll ans=0;
    for(int j=1;j<=k;j++) ans=(ans+f[n][j])%p;
    cout<<ans<<'\n';
    return 0;
}

ABC273E Notebook

题意

给出一个序列和一些备份，初始均为空。每次执行以下操作中的一个：

在当前序列中添加一个字母
将当前序列的最后一个字母删除
将当前序列存入一个备份
将当前序列替换为一个备份

问每次操作后的最后一个字母是多少。

题解

首先考虑最直接的模拟，即开若干个数组表示备份，将当前序列整个写入或者读出。但是这样时间复杂度会超，我们考虑简化。其实当我们存储备份的时候，我们只需要能根据它定位到原序列就行了，并不需要将整个序列都写进去，所以我们可以考虑标记一下该备份存储的是序列的哪一个位置。

但是，这些操作似乎仍然难以表示。一个比较巧妙的想法是构建一棵类似树的东西：

add操作，给当前结点添加一个儿子
del操作，从当前结点走向它的父亲
save操作，令 $pos_i=cur$
load操作，令 $cur=pos_i$

代码

#include <bits/stdc++.h>
using namespace std;
const int N=5e5+5;
int f[N],a[N];
map<int,int> pos;
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int id=0,cur=0,q;cin>>q;
    a[0]=-1;
    while(q--)
    {
        string s;cin>>s;
        if(s=="ADD")
        {
            int x;cin>>x;
            a[++id]=x;
            f[id]=cur;
            cur=id;
        }
        else if(s=="DELETE") cur=f[cur];
        else if(s=="SAVE")
        {
            int x;cin>>x;
            pos[x]=cur;
        }
        else 
        {
            int x;cin>>x;
            cur=pos[x];
        }
        cout<<a[cur]<<' ';
    }
    return 0;
}

ABC271E Subsequence Path

题意

给出一张有向图，求 $1$ 到 $n$ 的最短路。要求走的边的标号必须是给定序列 $E$ 的子序列。

题解

容易想歪的一道题目。其实它是个dp。（当时是有往这方面想的，但是没想下去。感觉这种被我忽视的念头往往是对的）

想到dp转移方程就很好写了，枚举序列中的每条边 $(u,v,w)$ ，有 $f_v=\min(f_v,f_u+w)$ 。

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=2e5+5;
struct edge
{
    int u,v,w;
}e[N];
ll f[N];
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    memset(f,0x3f,sizeof(f));
    f[1]=0;
    int n,m,k;cin>>n>>m>>k;
    for(int i=1;i<=m;i++) cin>>e[i].u>>e[i].v>>e[i].w;
    for(int i=1;i<=k;i++)
    {
        int x;cin>>x;
        int u=e[x].u,v=e[x].v,w=e[x].w;
        f[v]=min(f[v],f[u]+w);
    }
    cout<<(f[n]==0x3f3f3f3f3f3f3f3f?-1:f[n])<<'\n';
    return 0;
}

ABC267F Exactly K Steps

题意

给出一棵树， $k$ 次询问。每次询问 $(u,k)$ ，要求输出一个与结点 $u$ 距离为 $k$ 的点，若没有则输出 $-1$ 。

题解

首先考虑什么情况无解，显然是当距离 $u$ 最远的点与 $u$ 的距离都小于 $k$ 的时候。而距离树上某个点最远的点一定是直径的一个端点，所以我们就可以想到树的直径了。

将离线询问下来。我们先求出直径的两个端点，然后分别进行dfs，同时维护深度为 $k$ 的结点（任意一个就可以）。当遍历到的点有询问时，根据当前深度和询问找是否有这样的点就可以了。

代码

#include <bits/stdc++.h>
using namespace std;
typedef pair<int,int> pii;
const int N=2e5+5;
vector<int> g[N];
vector<pii> query[N];
int c,c1,c2,dis[N],node[N],ans[N];
void dfs(int u,int fa)
{
    for(auto v:g[u])
    {
        if(v==fa) continue;
        dis[v]=dis[u]+1;
        if(dis[v]>dis[c]) c=v;
        dfs(v,u);
    }
}
void diameter()
{
    dfs(1,0);
    c1=c;
    dis[c]=0,dfs(c,0);
    c2=c;
}
void dfs1(int u,int fa,int dep)
{
    node[dep]=u;
    for(auto i:query[u])
        if(dep-i.first>=0) ans[i.second]=node[dep-i.first];
    for(auto v:g[u])
    {
        if(v==fa) continue;
        dfs1(v,u,dep+1);
    }
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    memset(ans,-1,sizeof(ans));
    int n;cin>>n;
    for(int i=1;i<n;i++)
    {
        int u,v;cin>>u>>v;
        g[u].push_back(v),g[v].push_back(u);
    }
    int q;cin>>q;
    for(int i=1;i<=q;i++)
    {
        int u,k;cin>>u>>k;
        query[u].push_back({k,i});
    }
    diameter();
    dfs1(c1,0,0);
    dfs1(c2,0,0);
    for(int i=1;i<=q;i++) cout<<ans[i]<<'\n';
    return 0;
}

ABC266F Well-defined Path Queries on a Namori

题意

给出一张 $n$ 个点 $n$ 条边的简单无向连通图。每次询问 $x$ 到 $y$ 的简单路径是否唯一。

题解

读题的时候没注意到是个基环树…

注意到是个基环树的话题目就好做了。基环树可以看作是由一个环和环上的每个点沿伸出去的树组成。容易发现如果在同一个点的树内，路径是唯一的，否则不唯一。所以问题可以这样解决：先不断地删除度数为 $1$ 的点，剩下的点就是环上的点。然后以这些点为根进行dfs，将访问到的点都打上一种标记。每次询问时判断两个点的标记是否相同就可以了。

代码

#include <bits/stdc++.h>
using namespace std;
const int N=2e5+5;
vector<int> g[N];
int deg[N];
bool vis[N];
int id[N];
void dfs(int u,int fa)
{
    for(auto v:g[u])
    {
        if(!vis[v]||v==fa) continue;
        id[v]=id[u];
        dfs(v,u);
    }
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int n;cin>>n;
    for(int i=1;i<=n;i++)
    {
        int u,v;cin>>u>>v;
        g[u].push_back(v),g[v].push_back(u);
        deg[u]++,deg[v]++;
    }
    queue<int> q;
    for(int i=1;i<=n;i++)
        if(deg[i]==1) q.push(i);
    while(!q.empty())
    {
        int u=q.front();q.pop();
        vis[u]=1;
        for(auto v:g[u])
        {
            deg[v]--;
            if(deg[v]==1) q.push(v);
        }
    }
    for(int i=1;i<=n;i++)
        if(!vis[i]) 
        {
            id[i]=i;
            dfs(i,0);
        }
    int _;cin>>_;
    while(_--)
    {
        int x,y;cin>>x>>y;
        cout<<(id[x]==id[y]?"Yes":"No")<<'\n';
    }
    return 0;
}

ABC265E Warp

题意

高桥君初始在一个二维平面的原点，每次可以采取以下三种方式之一移动：

$(x,y)\to (x+a,y+b)$
$(x,y)\to (x+c,y+d)$
$(x,y)\to (x+e,y+f)$

平面中有 $m$ 个障碍点。求移动 $n$ 次的方案数。

题解

考虑dp。设 $f_{i,j,k}$ 为采用第一种方式 $i$ 次第二种方式 $j$ 次第三种方式 $k$ 次的方案数。则 $f_{i,j,k}=f_{i-1,j,k}+f_{i,j-1,k}+f_{i,j,k-1}$ 。

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+5;
const int p=998244353;
set<pair<int,int>> s;
ll dp[305][305][305];
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int n,m;cin>>n>>m;
    ll a,b,c,d,e,f;cin>>a>>b>>c>>d>>e>>f;
    for(int i=1;i<=m;i++)
    {
        int x,y;cin>>x>>y;
        s.insert({x,y});
    }
    dp[0][0][0]=1;
    for(int i=0;i<=n;i++)
        for(int j=0;j<=n-i;j++)
            for(int k=0;k<=n-i-j;k++)
            {
                ll x=i*a+j*c+k*e,y=i*b+j*d+k*f;
                if(s.count({x,y})) continue;
                if(i) dp[i][j][k]+=dp[i-1][j][k];
                if(j) dp[i][j][k]+=dp[i][j-1][k];
                if(k) dp[i][j][k]+=dp[i][j][k-1];
                dp[i][j][k]%=p;
            }
    ll ans=0;
    for(int i=0;i<=n;i++)
        for(int j=0;j<=n-i;j++) ans=(ans+dp[i][j][n-i-j])%p;
    cout<<ans<<'\n';
    return 0;
}

ABC264F Monochromatic Path

题意

有一个01矩阵。每次可以花费 $r_i$ 的代价翻转第 $i$ 行或 $c_i$ 的代价翻转第 $j$ 列。要求从左上角出发，每次向右或向下走，直到右下角，经过的所有格子数字必须相同，求最小代价。

题解

dp。其实想到怎么设计了，但是没继续想下去。

设 $f_{i,j,k,t}$ 表示访问到第 $i$ 行第 $j$ 列，第 $i$ 行是否翻转，第 $j$ 列是否翻转的最小代价。每次向右或向下转移，判断一下格子是否相同来决定是否需要翻转对应的列或行。

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=2005;
int r[N],c[N];
ll f[N][N][2][2];
char g[N][N];
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int h,w;cin>>h>>w;
    for(int i=1;i<=h;i++) cin>>r[i];
    for(int i=1;i<=w;i++) cin>>c[i];
    for(int i=1;i<=h;i++)
        for(int j=1;j<=w;j++) cin>>g[i][j];
    memset(f,0x3f,sizeof(f));
    f[1][1][0][0]=0,f[1][1][1][0]=r[1],f[1][1][0][1]=c[1],f[1][1][1][1]=r[1]+c[1];
    for(int i=1;i<=h;i++)
        for(int j=1;j<=w;j++)
            for(int k=0;k<=1;k++)
                for(int t=0;t<=1;t++)
                {
                    if((g[i][j]^k^t)==(g[i+1][j]^t)) f[i+1][j][0][t]=min(f[i+1][j][0][t],f[i][j][k][t]);
                    else f[i+1][j][1][t]=min(f[i+1][j][1][t],f[i][j][k][t]+r[i+1]);
                    if((g[i][j]^k^t)==(g[i][j+1]^k)) f[i][j+1][k][0]=min(f[i][j+1][k][0],f[i][j][k][t]);
                    else f[i][j+1][k][1]=min(f[i][j+1][k][1],f[i][j][k][t]+c[j+1]);
                }
    cout<<min({f[h][w][0][0],f[h][w][0][1],f[h][w][1][0],f[h][w][1][1]})<<'\n';
    return 0;
}

ABC263E Sugoroku 3

题意

一个人初始站在 $1$ 。当它位于 $i$ 时，会等概率地移动到 $i,i+1,\cdots,i+a_i$ 。求他走到 $n$ 的期望步数。

题解

显然是个dp。正向做是不容易的，因为我们没法知道有哪些点可以转移到目标点，转移的概率占总的多少，这样就算不了期望。但是，从一个点出发是已知的，它会等概率地转移到一些后继结点。所以我们可以这样设计状态：设 $f_i$ 为从 $i$ 走到 $n$ 的期望步数。有转移

f_i=1+\frac{1}{a_i+1}\sum_{k=i}^{i+a_i}f_k

把 $k=i$ 的项移过去

f_i=\frac{a_i+1}{a_i}+\frac{1}{a_i}\sum_{k=i+1}^{i+a_i}f_k

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=2e5+5;
const int p=998244353;
int a[N];
ll f[N],suf[N];
ll fpow(ll a,ll b)
{
    ll res=1;
    while(b)
    {
        if(b&1) res=res*a%p;
        a=a*a%p;
        b>>=1;
    }
    return res;
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int n;cin>>n;
    for(int i=1;i<=n-1;i++) cin>>a[i];
    for(int i=n-1;i;i--)
    {
        f[i]=(a[i]+1+suf[i+1]-suf[i+a[i]+1]+p)*fpow(a[i],p-2)%p;
        suf[i]=(suf[i+1]+f[i])%p;
    }
    cout<<f[1]<<'\n';
    return 0;
}

ABC262E Red and Blue Graph

题意

给出一张 $n$ 个点 $m$ 条边的无向简单图。将每个顶点涂成蓝色或红色。要求恰有 $k$ 个顶点被涂成红色，且有偶数条边连接颜色不同的顶点。求方案数。

题解

假设我们涂成红色的顶点为 $a_1,a_2,\cdots,a_k$ ，其中有 $x$ 对相邻，则连接颜色不同的顶点的边数为

\sum_{i=1}^kdeg_{a_i}-2x

注意到后一项是不影响奇偶性的，所以在涂成红色的顶点必然有偶数个度数为奇数，枚举一下就可以了。

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=2e5+5;
const int p=998244353;
int deg[N];
ll fac[N],ifac[N];
void init()
{
    fac[0]=1;
    for(int i=1;i<N;i++) fac[i]=i*fac[i-1]%p;
    ifac[0]=ifac[1]=1;
    for(int i=2;i<N;i++) ifac[i]=(p-p/i)*ifac[p%i]%p;
    for(int i=2;i<N;i++) ifac[i]=ifac[i]*ifac[i-1]%p;
}
ll C(ll n,ll m)
{
    if(n<m||m<0) return 0;
    return fac[n]*ifac[m]%p*ifac[n-m]%p;
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    init();
    int n,m,k;cin>>n>>m>>k;
    for(int i=1;i<=m;i++)
    {
        int u,v;cin>>u>>v;
        deg[u]++,deg[v]++;
    }
    int cnt1=0,cnt2=0;
    for(int i=1;i<=n;i++)
        if(deg[i]&1) cnt1++;
        else cnt2++;
    ll ans=0;
    for(int i=0;i<=min(cnt1,k);i+=2) ans=(ans+C(cnt1,i)*C(cnt2,k-i))%p;
    cout<<ans<<'\n';
    return 0;
}

ABC253F Operations on a Matrix

题意

给出一个 $n\times m$ 的矩阵，初始所有元素都是 $0$ 。有 $q$ 次询问，询问有以下三种类型：

1 l r x：给第 $l,l+1,\cdots,r$ 列所有元素加上 $x$ 。
2 i x：将第 $i$ 行所有元素换成 $x$ 。
3 i j：输出第 $i$ 行第 $j$ 列的元素。

题解

不难发现，我们需要将操作的时间视作一个维度，因为操作 $2$ 会令该行所有元素此前经历的操作 $1$ 被覆盖。由于本题可以离线，所以就这样一个思路：将询问离线下来，依次处理每一列。同时，我们用一个树状数组维护所有时刻的 $1$ 操作。容易想到将操作 $1$ 差分一下，插入时间轴上的对应位置。对于操作 $2$ ，我们记录下值和前驱。对于操作 $3$ ，我们查询前驱和当前操作之间树状数组上的值（就是未被覆盖的操作 $1$ 的和），再加上该操作前的最后一次操作 $2$ 的值就可以了。

具体细节可以参考代码。

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=2e5+5;
int n,m,q;
ll c[N];
int lowbit(int x) {return x&-x;}
void add(int x,int k)
{
    while(x<=q)
    {
        c[x]+=k;
        x+=lowbit(x);
    }
}
ll query(int x)
{
    if(!x) return 0;
    ll ans=0;
    while(x)
    {
        ans+=c[x];
        x-=lowbit(x);
    }
    return ans;
}
struct op
{
    int idx,val,dfn,pre;
    bool operator < (const op x) {return idx==x.idx?pre<x.pre:idx<x.idx;}
}o[2*N];
int cnt,tot,cur[N],val[N],id[N];
ll ans[N];
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cin>>n>>m>>q;
    for(int i=1;i<=q;i++)
    {
        int op;cin>>op;
        if(op==1)
        {
            int l,r,x;cin>>l>>r>>x;
            o[++cnt]={l,x,i,-1};
            o[++cnt]={r+1,-x,i,-1};
        }
        else if(op==2)
        {
            int j,x;cin>>j>>x;
            cur[j]=i;
            val[j]=x;
        }
        else
        {
            int x,y;cin>>x>>y;
            o[++cnt]={y,val[x],i,cur[x]};
            id[i]=++tot;
        }
    }
    sort(o+1,o+cnt+1);
    for(int i=1;i<=cnt;i++)
    {
        if(o[i].pre==-1) add(o[i].dfn,o[i].val);
        else ans[id[o[i].dfn]]=query(o[i].dfn)-query(o[i].pre)+o[i].val;
    }
    for(int i=1;i<=tot;i++) cout<<ans[i]<<'\n';
    return 0;
}

ABC245E Wrapping Chocolate

题意

有 $n$ 块巧克力，大小为 $a_i\times b_i$ 。有 $m$ 个盒子，大小为 $c_i\times d_i$ 。一块巧克力能被放进盒子当且仅当 $a_i\leq c_i,b_i\leq d_i$ 。每个盒子最多只能放一块巧克力。问所有的巧克力是否都能被放进盒子里。

题解

感觉贪心水平有待提高，这应该是个挺典的题目。

将所有巧克力和盒子按第一维从大到小排序，相同的按第二维从大到小，再相同的盒子排在巧克力前面。我们用一个map维护可选用的第二维，每当遇到一个盒子时，mp[d[i]]++，每当遇到一块巧克力时，在map中二分查找不小于b[i]的最小元素，若没有则是No。

代码

#include <bits/stdc++.h>
using namespace std;
const int N=2e5+5;
struct node
{
    int x,y,flag;
    bool operator < (const node a)
    {
        if(x==a.x)
        {
            if(y==a.y)
                return flag<a.flag;
            return y>a.y;
        }
        return x>a.x;
    }
}nodes[2*N];
int a[N],b[N],c[N],d[N];
map<int,int> mp;
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int n,m;cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>a[i];
    for(int i=1;i<=n;i++) cin>>b[i];
    for(int i=1;i<=m;i++) cin>>c[i];
    for(int i=1;i<=m;i++) cin>>d[i];
    for(int i=1;i<=n;i++) nodes[i]={a[i],b[i],1};
    for(int i=n+1;i<=n+m;i++) nodes[i]={c[i-n],d[i-n],0};
    sort(nodes+1,nodes+n+m+1);
    for(int i=1;i<=n+m;i++)
    {
        if(!nodes[i].flag) mp[nodes[i].y]++;
        else
        {
            auto it=mp.lower_bound(nodes[i].y);
            if(it==mp.end())
            {
                cout<<"No"<<'\n';
                return 0;
            }
            int x=it->first;
            mp[x]--;
            if(!mp[x]) mp.erase(x);
        }
    }
    cout<<"Yes"<<'\n';
    return 0;
}

ABC243E Edge Deletion

题意

给出一张无向图，问最多可以删除多少条边，使得图仍然连通且任意两点间最短距离不变。

题解

一个朴素的想法是枚举每条边是否能删除，然后跑全源最短路。可以做到 $O(n^4)/O(n^3\log n)$ 。更好的做法是先跑Floyd求出全源最短路。然后对于每条边，看是否存在一个点能将它松弛。如果存在，那么这条边就可以被删除。

代码

#include <bits/stdc++.h>
using namespace std;
const int N=305;
int d[N][N];
bool vis[N][N];
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    memset(d,0x3f,sizeof(d));
    int n,m;cin>>n>>m;
    for(int i=1;i<=n;i++) d[i][i]=0;
    for(int i=1;i<=m;i++)
    {
        int u,v,w;cin>>u>>v>>w;
        d[u][v]=d[v][u]=w;
        vis[u][v]=vis[v][u]=1;
    }
    for(int k=1;k<=n;k++)
        for(int i=1;i<=n;i++)
            for(int j=1;j<=n;j++)
                d[i][j]=min(d[i][j],d[i][k]+d[k][j]);
    int ans=0;
    for(int i=1;i<=n;i++)
        for(int j=i+1;j<=n;j++)
            for(int k=1;k<=n;k++)
                if(vis[i][j]&&k!=i&&k!=j&&d[i][j]==d[i][k]+d[k][j])
                {
                    ans++;
                    break;
                }
    cout<<ans<<'\n';
    return 0;
}

ABC239F Construct Highway

题意

给定 $n$ 个点的度数 $d_i$ ，再给定 $m$ 条边。要求构造一棵树，满足包含所有给定的边并且点 $i$ 的度数为 $d_i$ 。

题解

猜结论的题目。

首先需要满足 $\sum\limits_{i=1}^nd_i=2\times (n-1)$ ，否则无解。然后考虑给定的边，它们构成了一些连通块。由于我们要构成一棵树，所以边一定是在连通块之间。对于一个连通块，我们维护它里面的点还缺了多少度数，如果有点的度数已经溢出了，那么也无解。否则我们按以下流程操作：对于连通块，我们按需要分配的总度数是否大于 $1$ 分为两类，每次从大于 $1$ 的连向恰为 $1$ 的，直到最终剩下两个恰好为 $1$ 的。最后再判断一下整张图是否连通。

具体判断细节还是比较多的，需要想清楚。

代码

#include <bits/stdc++.h>
using namespace std;
const int N=2e5+5;
int d[N],f[N];
vector<int> v[N];
vector<int> v1;
vector<vector<int>> v2;
vector<pair<int,int>> ans;
int find(int x) {return f[x]==x?x:f[x]=find(f[x]);}
void merge(int x,int y)
{
    x=find(x),y=find(y);
    if(x==y) return;
    f[x]=y;
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int n,m;cin>>n>>m;
    int sum=0;
    for(int i=1;i<=n;i++) cin>>d[i],sum+=d[i];
    for(int i=1;i<=n;i++) f[i]=i;
    for(int i=1;i<=m;i++)
    {
        int u,v;cin>>u>>v;
        d[u]--,d[v]--;
        merge(u,v);
    }
    if(sum!=2*(n-1))
    {
        cout<<-1<<'\n';
        return 0;
    }
    for(int i=1;i<=n;i++)
    {
        if(d[i]<0)
        {
            cout<<-1<<'\n';
            return 0;
        }
        for(int j=1;j<=d[i];j++) v[find(i)].push_back(i);
    }
    for(int i=1;i<=n;i++)
    {
        if((int)v[i].size()==1) v1.push_back(v[i][0]);
        if((int)v[i].size()>1) v2.push_back(v[i]);
    }
    for(auto i:v2)
    {
        for(int j=1;j<(int)i.size();j++)
        {
            if(v1.empty())
            {
                cout<<-1<<'\n';
                return 0;
            }
            merge(i[j],v1.back());
            ans.push_back({i[j],v1.back()});
            v1.pop_back();
        }
        v1.push_back(i[0]);
    }
    if((int)v1.size()>2) 
    {
        cout<<-1<<'\n';
        return 0;
    }
    merge(v1[0],v1[1]);
    ans.push_back({v1[0],v1[1]});
    for(int i=1;i<=n;i++)
        if(find(i)!=find(1))
        {
            cout<<-1<<'\n';
            return 0;
        }
    for(auto i:ans) cout<<i.first<<' '<<i.second<<'\n';
    return 0;
}

ABC236E Average and Median

题意

给出一个数组，要求相邻两个元素至少选一个。求选出元素的最大平均值和最大中位数。

题解

二分+dp。

二分平均值 $x$ ，令 $b_i=a_i-x$ 。令 $f_{i,0/1}$ 为前 $i$ 个元素第 $i$ 个不选/选的最大值，转移显然，最终 $\max(f_{i,0},f_{i,1})>0$ 即符合。这里涉及到浮点数二分，比较简单的写法是固定一个二分次数。

二分中位数 $x$ ，若 $a_i\geq x$ 则 $b_i=1$ ，否则 $b_i=-1$ 。其余相同。这里只需要整数二分。

代码

#include <bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int n,a[N];
double b[N],f[N][2];
bool check()
{
    for(int i=1;i<=n;i++)
    {
        f[i][0]=f[i-1][1];
        f[i][1]=max(f[i-1][0],f[i-1][1])+b[i];
    }
    return max(f[n][0],f[n][1])>0;
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cin>>n;
    for(int i=1;i<=n;i++) cin>>a[i];
    double l=0,r=1e9,ans1;
    for(int _=1;_<=250;_++)
    {
        double m=(l+r)/2;
        for(int i=1;i<=n;i++) b[i]=a[i]-m;
        if(check()) ans1=m,l=m;
        else r=m;
    }
    cout<<fixed<<setprecision(10)<<ans1<<'\n';
    int ll=0,rr=1e9;
    while(ll<rr)
    {
        int m=(ll+rr+1)/2;
        for(int i=1;i<=n;i++)
            if(a[i]<m) b[i]=-1;
            else b[i]=1;
        if(check()) ll=m;
        else rr=m-1;
    }
    cout<<ll<<'\n';
    return 0;
}

ABC232F Simple Operations on Sequence

题意

给定两个序列 $a$ 和 $b$ ，每次可以执行以下两种操作中的一种：

令 $a_i$ 加一或减一，代价为 $X$ 。
交换 $a_i$ 和 $a_{i+1}$ ，代价为 $Y$ 。

求将序列 $a$ 变成 $b$ 需要的最小代价。

数据范围： $n\leq 18$ 。

题解

看到数据范围就想到状压，不过我们需要分析一下为什么能状压。

设最终的 $a$ 为 $a_{p_1},a_{p_2},\cdots,a_{p_n}$ 。那么总的代价为

\sum_{i=1}^n|a_{p_i}-b_i|+inv(P)

$inv(P)$ 为排列 $\{p_1,p_2,\cdots,p_n\}$ 中的逆序对数量。

可以化简为

\sum_{i=1}^n(|a_{p_i}-b_i|+\sum_{j<i}[p_j>p_i])

我们发现，当我们进行转移时，我们只关心哪些 $p_i$ 是被选取的，并不关心它的顺序（因为一定是从最优的转移，它的顺序对转移没有影响）。所以我们可以用 $S$ 表示哪些 $p_i$ 被选择，从而进行状压dp。

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=20;
ll a[N],b[N],f[(1<<20)+5];
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int n;ll x,y;cin>>n>>x>>y;
    for(int i=1;i<=n;i++) cin>>a[i];
    for(int i=1;i<=n;i++) cin>>b[i];
    memset(f,0x3f,sizeof(f));
    f[0]=0;
    for(int s=0;s<(1<<n);s++)
    {
        int cnt1=0;
        for(int i=1;i<=n;i++)
            if(s>>(i-1)&1) cnt1++;
        for(int i=1;i<=n;i++)
        {
            int cnt2=0;
            for(int j=i+1;j<=n;j++)
                if(s>>(j-1)&1) cnt2++;
            f[s|(1<<(i-1))]=min(f[s|(1<<(i-1))],f[s]+abs(a[i]-b[cnt1+1])*x+cnt2*y);
        }
    }
    cout<<f[(1<<n)-1]<<'\n';
    return 0;
}

ABC227D Project Planning

题意

有 $n$ 个部门，每个部门有 $a_i$ 个员工。每项活动需要 $k$ 个来自不同部门的员工，求最多能安排多少项活动。

题解

感觉是很典的一道题，但是不会。

思路很简单：二分答案。在check时，当前需要 $m$ 项活动，那么记 $sum=\sum\limits_{i=1}^n\min(a_i,m)$ 。判断 $sum\geq m\times k$ 即可。

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=2e5+5;
int n,k;
ll a[N];
bool check(ll m)
{
    ll sum=0;
    for(int i=1;i<=n;i++) sum+=min(a[i],m);
    return sum>=(__int128)m*k;
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cin>>n>>k;
    for(int i=1;i<=n;i++) cin>>a[i];
    ll l=0,r=1e18;
    while(l<r)
    {
        ll m=(l+r+1)/2;
        if(check(m)) l=m;
        else r=m-1;
    }
    cout<<l<<'\n';
    return 0;
}

ABC225E 7

题意

平面的第一象限有一些 7。7 被定义为两条线段，连接 $(x_i-1,y_i),(x_i,y_i)$ 和 $(x_i,y_i-1),(x_i,y_i)$ 。要求删除一些 7，使得尽可能多的 7 完全可见。

7 完全可见被定义为原点，7 的三个顶点构成的四边形内部不与其它的 7 相交。

题解

对于每个 $7$ ，我们关心 $(0,0),(x_i-1,y_i),(x_i,y_i-1)$ 构成的三角形，如果三角形与别的三角形相交，那么它就不是完全可见的。

判断三角形相交可以通过比较两条边斜率的方式，若 $\dfrac{y_i-1}{x_i}$ 与 $\dfrac{y_i}{x_i-1}$ 间还有别的斜率，那么这个三角形就是不完全可见的。这就转换为了线段覆盖问题，两个斜率就是线段的两个端点。按照右端点排序以后贪心解决。

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=2e5+5;
struct node
{
    ll x,y;
    ll xx,yy;
    bool operator < (const node &t) const {return yy*t.xx<t.yy*xx;}
}arr[N];
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int n;cin>>n;
    for(int i=1;i<=n;i++)
    {
        int a,b;cin>>a>>b;
        arr[i]={a,b-1,a-1,b};
    }
    sort(arr+1,arr+n+1);
    int ans=0,l=0;
    for(int i=1;i<=n;i++)
        if(arr[i].y*arr[l].xx>=arr[l].yy*arr[i].x)
        {
            ans++;
            l=i;
        }
    cout<<ans<<'\n';
    return 0;
}