网络流简介

网络

网络是指一个有向图 $G=(V,E)$ 。

每条边 $(u,v)\in E$ 都有一个权值 $c(u,v)$ ，称之为容量。当 $(u,v)\notin E$ 时有 $c(u,v)=0$ 。

其中有两个特殊的点：源点 $s\in V$ 和汇点 $t\in V,(s\neq t)$ 。

流

设 $f(u,v)$ 定义在二元组 $(u\in V,v\in V)$ 上的实数函数且满足

容量限制：对于每条边，流经该边的流量不得超过该边的容量，即 $f(u,v)\leq c(u,v)$ 。
斜对称性：每条边的流量与其相反边的流量之和为 $0$ ，即 $f(u,v)=-f(v,u)$ 。
流守恒性：从源点流出的流量等于汇点流入的流量，即 $\forall x\in V-\{s,t\},\sum_{(u,x)\in E}f(u,x)=\sum_{(x,v)\in E}f(x,v)$ 。

那么 $f$ 称为网络 $G$ 的流函数。对于 $(u,v)\in E$ ， $f(u,v)$ 称为边的流量， $c(u,v)-f(u,v)$ 称为边的剩余容量。整个网络的流量为 $\sum_{(s,v)\in E}f(s,v)$ ，即从源点出发的所有流量之和。

流函数的完整定义为

f(u,v)= \left\{ \begin{aligned} &f(u,v),&(u,v)\in E\\ &-f(v,u),&(v,u)\in E\\ &0,&(u,v)\notin E,(v,u)\notin E \end{aligned} \right.

网络流的常见问题

最大流：我们有一张图，要求从源点流向汇点的最大流量（可以有很多条路到达汇点），就是我们的最大流问题。

最小割：割其实就是删边的意思，当然就是割就是割掉 $X$ 条边让 $S$ 跟 $T$ 不互通。我们要求 $X$ 条边加起来的流量总和最小。这就是最小割问题。

最小费用最大流：最小费用最大流问题是这样的：每条边都有一个费用，代表单位流量流过这条边的开销。我们要在求出最大流的同时，要求花费的费用最小。

网络流24题

最大流

概念补充

###残量网络

首先我们介绍一下一条边的剩余容量 $c_f(u,v)$ ，它表示的是这条边的容量与流量之差，即 $c_f(u,v)=c(u,v)-f(u,v)$ 。

对于流函数 $f$ ，残量网络 $G_f$ 是网络 $G$ 中所有结点和剩余容量大于0的边构成的子图。形式化的定义，即 $G_f=(V_f=V,E_f=\{(u,v\in E,c_f(u,v)>0\})$ 。

注意，剩余容量大于 $0$ 的边可能不在原图 $G$ 中（流函数的斜对称性，残量网络中可能包括虚边）。

增广路

在原图 $G$ 中若一条从源点到汇点的路径上所有边的剩余容量都大于0，这条路被称为增广路。

或者说，在残量网络 $G_f$ 中，一条从源点到汇点的路径被称为增广路。

###反向边

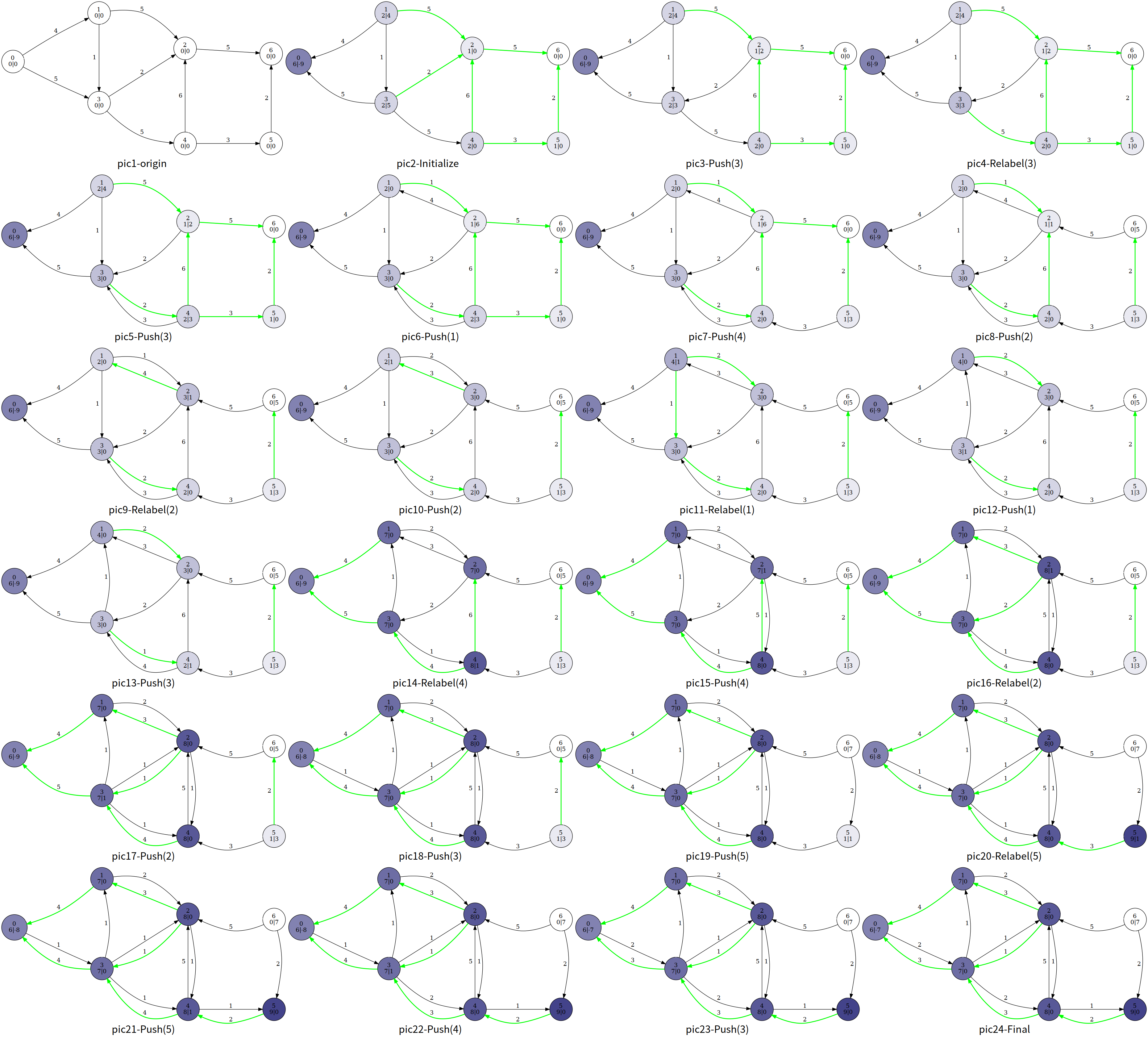
建立反向边相当于提供了“后悔机制“，因为我们一开始选择的边未必是最优的。

1673142566409

以上图为例， $1\to 2\to 4\to 6$ 这条增广路流量为 $5$ ，建立对应的反向边。在残量网络中存在 $1\to 3\to 4\to 2\to 5$ 这条流量为 $2$ 的增广路。这时我们就用到了 $4\rightarrow 2$ 这条反向边。它的实际意义是从结点 $2$ 到结点 $4$ 的流量减少 $2$ ，结点 $2$ 的流量转而流向结点 $5$ ，结点 $4$ 的流量由结点 $3$ 补充。由此，实现了对之前决策的修正。

Dinic算法

Dinic算法的过程是这样的：在每次增广前，先用bfs将图分层。然后用dfs寻找增广路。

算法时间复杂度为 $O(n^2m)$ 。在稀疏图上效率和EK算法相当，但在稠密图上效率比EK算法高很多。

前置知识

EK算法（自行学习）。

优化

当前弧优化：对于一个结点 $x$ ，当它在dfs中走到第 $i$ 条弧时，前 $i-1$ 条弧到汇点的流一定已经流满，那么下一次访问 $x$ 节点时前 $i-1$ 条弧就没有意义了。
余量优化：当余量为 $0$ 时，不必再访问后继结点。
残枝优化：若一个点无法到达汇点，将该点踢出图层。

代码实现

const int inf=0x3f3f3f3f;
struct edge
{
    int to,nxt;
    int c;
}e[2*maxm];
int cnt=1,head[maxn];
int s,t;
int d[maxn],cur[maxn];
void add(int u,int v,int c)
{
    e[++cnt]={v,head[u],c};head[u]=cnt;
    e[++cnt]={u,head[v],0};head[v]=cnt;
}
bool bfs()
{
    memset(d,0,sizeof(d));
    queue<int> q;
    d[s]=1;q.push(s);
    while(!q.empty())
    {
        int u=q.front();q.pop();
        for(int i=head[u];i;i=e[i].nxt)
        {
            int v=e[i].to;
            if(d[v]==0&&e[i].c)
            {
                d[v]=d[u]+1;q.push(v);
                if(v==t) return true;
            }
        }
    }
    return false;
}
int dfs(int u,int mf)
{
    if(u==t) return mf;
    int sum=0;
    for(int i=cur[u];i;i=e[i].nxt)
    {
        cur[u]=i;
        int v=e[i].to;
        if(d[v]==d[u]+1&&e[i].c)
        {
            int res=dfs(v,min(mf,e[i].c));
            e[i].c-=res;
            e[i^1].c+=res;
            sum+=res;
            mf-=res;
            if(mf==0) break;
        }
    }
    if(sum==0) d[u]=0;
    return sum;
}
int dinic()
{
    int flow=0;
    while(bfs())
    {
        memcpy(cur,head,sizeof(cur));
        flow+=dfs(s,inf);
    }
    return flow;
}

预流推进

主要思想

预流推进算法通过对单个结点的更新操作，直到没有结点需要更新来求解最大流。

算法过程维护的流函数不一定保持流守恒性，对于一个结点，我们允许进入结点的流超过流出结点的流，超过的部分被称为结点 $u(u\in V-{s,t})$ 的超额流 $e(u)$ ：

e(u)=\sum_{(x,u)\in E}f(x,u)-\sum_{(u,y)\in E}f(u,y)

若 $u>0$ ，称结点 $u$ 溢出。注意当我们提到溢出结点时，并不包括 $s$ 和 $t$ 。

预流推进算法维护每个结点的高度 $h(u)$ ，并且规定溢出的结点 $u$ 如果要推送超额流，只能向高度小于 $u$ 的结点推送；如果 $u$ 没有相邻的高度小于 $u$ 的结点，就修改 $u$ 的高度（重贴标签）。

###具体细节

高度函数

预流推进维护以下的一个映射 $h:V\to \mathbf{N}$ ：

$h(s)=|V|,h(t)=0$
$\forall (u,v)\in E_f,h(u)\leq h(v)+1$

称 $h$ 是残量网络 $G_f=(V_f,E_f)$ 的高度函数。

引理1：设 $G_f$ 上的高度函数为 $h$ ，对于任意两个结点 $u,v\in V$ ，如果 $h(u)>h(v)+1$ ，则 $(u,v)$ 不是 $G_f$ 中的边。

算法只会在 $h(u)=h(v)+1$ 的边执行推送。

推送

适用条件：结点 $u$ 溢出，且存在结点 $v$ 满足 $(u,v)\in E,c(u,v)-f(u,v)>0,h(u)=h(v)+1$ ，则推送操作适用于 $(u,v)$ 。

于是，我们尽可能将超额流从 $u$ 推送到 $v$ ，推送过程中我们只关心超额流和 $c(u,v)-f(u,v)$ 的最小值，不关心 $v$ 是否溢出。

如果 $(u,v)$ 在推送完之后满流，将其从残量网络中删除。

重贴标签

适用条件：如果结点 $u$ 溢出，且 $\forall (u,v)\in E_f,h(u)\leq h(v)$ ，则重贴标签操作适用于 $u$ 。

将 $h(u)$ 更新为 $min_{(u,v)\in E_f}h(v)+1$ 即可。

初始化

\begin{aligned} \forall (u,v)\in E,&f(u,v)=\left\{\begin{aligned} &c(u,v)&,u=s\\ &0&,u\neq s \end{aligned}\right. \\ \forall u\in V,&h(u)=\left\{\begin{aligned} &|V|&,u=s\\ &0&,u\neq s\\ \end{aligned}\right. ,e(u)=\sum_{(x,u)\in E}f(x,u)-\sum_{(u,y)\in E}f(u,y) \end{aligned}

上述将 $(s,v)\in E$ 充满流，并将 $h(s)$ 抬高，使得 $(s,v)\notin E_f$ ，因为 $h(s)>h(v)$ ，而 $(s,v)$ 已经满流，没必要留在残量网络中；上述还将 $e(s)$ 初始化为 $\sum_{(s,v)\in E}f(s,v)$ 的相反数。

HLPP算法

HLPP算法是在预流推进算法的基础上，每次选择高度最高的溢出结点进行推送。

算法时间复杂度为 $O(n^2\sqrt{m})$ 。

过程

初始化（基于预流推进算法）；
选择溢出结点中高度最高的结点 $u$ ，并对它所有可以推送的边进行推送；
如果 $u$ 仍溢出，对它重贴标签，回到步骤2；
如果没有溢出的结点，算法结束。

###bfs优化

在初始化时，将 $h(u)$ 设置为 $u$ 到 $t$ 的最短距离；特别地， $h(s)=n$ 。

gap优化

推送的条件是 $h(u)=h(v)+1$ ，而如果在算法的某一时刻， $h(u)=x$ 的结点个数为 $0$ ，那么对于 $h(u)>x$ 的结点就永远无法推送超额流到 $t$ ，因此只能送回 $s$ ，那么我们就在这时直接让他们的高度变成至少 $n+1$ ，以尽快推送回 $s$ ，减少重贴标签的操作。

HLPP

pic13到pic14时，将结点 $6$ 高度修改为 $4$ 后，没有高度为 $2$ 的点了，所以要对高度大于 $2$ 的点进行gap优化。

###其它优化

事实上只需要维护高度小于 $n$ 的结点也能获得正确的最大流。考虑高度为 $n$ 的结点，其溢出流被推送到汇点 $t$ 需要沿一条高度分别为 $n,n-1,\cdots,0$ 的结点构成的路径，这显然时不存在的。

但是这样操作的代价是算法终止时会有一些结点的溢出流不为零，因此不能求出每条边上的真实流量。

代码实现

const int inf=0x3f3f3f3f;
int n,m,s,t;
struct Edge
{
    int to,nxt;
    int c;
}e[2*maxm];
int cnt=1,head[maxn];
void add(int u,int v,int c)
{
    e[++cnt]={v,head[u],c};head[u]=cnt;
    e[++cnt]={u,head[v],0};head[v]=cnt;
}
int h[maxn],gap[maxn];
int ex[maxn];
stack<int> B[maxn];
int level=0;
int push(int u)
{
    bool flag=(u==s);
    for(int i=head[u];i;i=e[i].nxt)
    {
        int v=e[i].to;int c=e[i].c;
        if(!c||(!flag&&h[u]!=h[v]+1)) continue;
        int k=(flag?c:min(c,ex[u]));
        if(v!=s&&v!=t&&!ex[v]) B[h[v]].push(v),level=max(level,h[v]);
        ex[u]-=k,ex[v]+=k,e[i].c-=k,e[i^1].c+=k;
        if(!ex[u]) return 0;
    }
    return 1;
}
void relabel(int u)
{
    h[u]=inf;
    for(int i=head[u];i;i=e[i].nxt)
        if(e[i].c) h[u]=min(h[u],h[e[i].to]);
    if(++h[u]<n)
    {
        B[h[u]].push(u);
        level=max(level,h[u]);
        gap[h[u]]++;
    }
}
bool bfs()
{
    memset(h,0x3f,sizeof(h));
    queue<int> q;
    h[t]=0;q.push(t);
    while(!q.empty())
    {
        int u=q.front();q.pop();
        for(int i=head[u];i;i=e[i].nxt)
        {
            int v=e[i].to;
            if(e[i^1].c&&h[v]>h[u]+1) h[v]=h[u]+1,q.push(v);
        }
    }
    return h[s]!=inf;
}
int select()
{
    while(B[level].empty()&&level>-1) level--;
    return level==-1?0:B[level].top();
}
int hlpp()
{
    if(!bfs()) return 0;
    memset(gap,0,sizeof(gap));
    for(int i=1;i<=n;i++)
        if(h[i]!=inf) gap[h[i]]++;
    h[s]=n;push(s);
    int u;
    while((u=select()))
    {
        B[level].pop();
        if(push(u))
        {
            if(!--gap[h[u]])
                for(int i=1;i<=n;i++)
                    if(i!=s&&i!=t&&h[i]>h[u]&&h[i]<n+1)
                        h[i]=n+1;
            relabel(u);
        }
    }
    return ex[t];
}

练习

Luogu P2065 [TJOI2011] 卡片

Luogu P2763 试题库问题

Luogu P2472 [SCOI2007] 蜥蜴

Luogu P2754 [CTSC1999]家园 / 星际转移问题

Luogu P2765 魔术球问题

最小割

概念补充

割

对于一个网络流图 $G=(V,E)$ ，其割的定义为一种点的划分方式：将所有的点划分为 $S$ 和 $T=V-S$ 两个集合，其中源点 $s\in S$ ，汇点 $t\in T$ 。

割的容量

我们定义割 $(S,T)$ 的容量 $c(S,T)$ 表示所有从 $S$ 到 $T$ 的边的容量之和，即 $c(S,T)=\sum_{u\in S,v\in T}c(u,v)$ 。

最小割

最小割就是求得一个割 $(S,T)$ 使得割的容量 $c(S,T)$ 最小。

最大流最小割定理

f_{max}=c(S,T)_{min}

引理1：对于图 $G$ 的任意一个割 $c(S,T)$ ，有 $f_{max}\leq c(S,T)$ 。

引理2：最大流 $f_{max}$ 对应的残量网络 $G_f$ 中，取从源点 $s$ 出发能到达的所有点为 $S$ ， $V-S$ 为 $T$ ，则 $c(S,T)$ 为最小割。

（具体证明略）

练习

Luogu P1344 [USACO4.4]追查坏牛奶Pollutant Control

Luogu P1345 [USACO5.4]奶牛的电信Telecowmunication

Luogu P2057 [SHOI2007] 善意的投票 / [JLOI2010] 冠军调查

Luogu P2598 [ZJOI2009]狼和羊的故事

Luogu P2774 方格取数问题

Luogu P4126 [AHOI2009]最小割

Luogu P5039 [SHOI2010]最小生成树

Luogu P2805 [NOI2009] 植物大战僵尸

Luogu P3749 [六省联考 2017] 寿司餐厅

费用流

概念补充

给定一个网络 $G=(V,E)$ ，每条边除了有容量限制 $c(u,v)$ ，还有一个单位流量的费用 $w(u,v)$ 。

当 $(u,v)$ 的流量为 $f(u,v)$ 时，需要花费 $f(u,v)\times w(u,v)$ 的费用。

$w$ 也满足斜对称性，即 $w(u,v)=-w(v,u)$ 。

则该网络中总花费最小的最大流称为最小费用最大流。

SSP算法

SSP算法是一个贪心的算法。它的思路是每次寻找单位费用最小的增广路进行增广，直到图上不存在增广路为止。

设该网络的最大流为 $f$ ，则最坏时间复杂度为 $O(nmf)$ 。

代码实现

const int inf=0x3f3f3f3f;
struct edge
{
    int to,nxt;
    int c,w;
}e[2*maxm];
int cnt=1,head[maxn];
int s,t;
int flow,val;
int d[maxn],vis[maxn],cur[maxn];
void add(int u,int v,int c,int w)
{
    e[++cnt]={v,head[u],c,w};head[u]=cnt;
    e[++cnt]={u,head[v],0,-w};head[v]=cnt;
}
bool spfa()
{
    memset(d,0x3f,sizeof(d));
    queue<int> q;
    q.push(s);d[s]=0;vis[s]=1;
    while(!q.empty())
    {
        int u=q.front();q.pop();vis[u]=0;
        for(int i=head[u];i;i=e[i].nxt)
        {
            int v=e[i].to;
            if(d[v]>d[u]+e[i].w&&e[i].c)
            {
                d[v]=d[u]+e[i].w;
                if(!vis[v]) q.push(v),vis[v]=1;
            }
        }
    }
    return d[t]!=inf;
}
int dfs(int u,int mf)
{
    if(u==t) return mf;
    vis[u]=1;
    int sum=0;
    for(int i=cur[u];i;i=e[i].nxt)
    {
        cur[u]=i;
        int v=e[i].to;
        if(!vis[v]&&d[v]==d[u]+e[i].w&&e[i].c)
        {
            int res=dfs(v,min(mf,e[i].c));
            e[i].c-=res;e[i^1].c+=res;
            sum+=res;
            val+=res*e[i].w;
            mf-=res;
            if(mf==0) break;
        }
    }
    if(sum==0) d[u]=0;
    vis[u]=0;
    return sum;
}
void ssp()
{
    while(spfa())
    {
        memcpy(cur,head,sizeof(cur));
        flow+=dfs(s,inf);
    }
}

练习

Luogu P4016 负载平衡问题

Luogu P2045 方格取数加强版

Luogu P2053 [SCOI2007] 修车

Luogu P2050 [NOI2012] 美食节

Luogu P2604 [ZJOI2010]网络扩容

Luogu P3159 [CQOI2012]交换棋子

上下界网络流

上下界网络流本质是给流量网络的每一条边设置了流量上界 $c(u,v)$ 和流量下界 $b(u,v)$ 。也就是说，一种可行的流必须满足 $b(u,v)\leq f(u,v)\leq c(u,v)$ 。同时必须满足除了源点和汇点之外的其余点流量平衡。

无源汇上下界可行流

给定无源汇流量网络 $G$ 。询问是否存在一种标定每条边流量的方式，使得每条边流量满足上下界同时每一个点流量平衡。

不妨假设每条边已经流了 $b(u,v)$ 的流量，设其为初始流。同时我们在新图中加入 $u$ 连向 $v$ 的流量为 $c(u,v)-b(u,v)$ 的边。考虑在新图上进行调整。

构造出来的初始流很有可能不满足流量平衡。假设一个点初始流入流量减初始流出流量为 $M$ 。

若 $M=0$ ，此时流量平衡，不需要附加边。

若 $M>0$ ，此时入流量过大，需要新建附加源点 $S'$ ， $S'$ 向其连流量为 $M$ 的附加边。

若 $M<0$ ，此时出流量过大，需要新建附加汇点 $T'$ ，其向 $T'$ 连流量为 $-M$ 的附加边。

如果附加边满流，说明这一个点的流量平衡条件可以满足，否则这个点的流量平衡条件不满足。（因为原图加上附加流之后才会满足原图中的流量平衡。举个例子：原图中 $M>0$ ，如果 $S'$ 连向该点的边满流，则该点又向外流出了 $M$ 的流量，与原图叠加就满足平衡了。）

所以在建图完毕之后跑 $S'$ 到 $T'$ 的最大流，若 $S'$ 连出去的边全部满流，则存在可行流，否则不存在。

有源汇上下界可行流

给定有源汇流量网络 $G$ 。询问是否存在一种标定每条边流量的方式，使得每条边流量满足上下界同时除了源点和汇点每一个点流量平衡。

假设源点为 $S$ ，汇点为 $T$ 。则我们可以加入一条 $T$ 到 $S$ 的上界为 $\infin$ ，下界为 $0$ 的边转化为无源汇上下界可行流问题。（因为 $S$ 只有流出， $T$ 只有流入）

若有解，则 $S$ 到 $T$ 的可行流流量等于 $T$ 到 $S$ 的附加边的流量。

##有源汇上下界最大流

给定有源汇流量网络 $G$ 。询问是否存在一种标定每条边流量的方式，使得每条边流量满足上下界同时除了源点和汇点每一个点流量平衡。如果存在，询问满足标定的最大流量。

我们找到网络上的任意一个可行流。如果找不到解就可以直接结束。

否则我们考虑删去所有附加边之后的残量网络并且在网络上进行调整。

我们在残量网络上再跑一次 $S$ 到 $T$ 的最大流，将可行流流量和最大流流量相加即为答案。

#include <bits/stdc++.h>
using namespace std;
#define inf 1000000000000000
#define V 100010
#define E 500010
typedef long long int ll;
struct edge {
	int to, next;
	ll capa;
};
int cnt = 0, head[V], n, m, st, ed; edge node[E];
inline void add(int fir, int nxt, ll w) {
	node[cnt].to = nxt,
		node[cnt].capa = w,
		node[cnt].next = head[fir],
		head[fir] = cnt++;
}
int s, t, dep[V], gap[V], cur[V]; queue<int>que; ll sum = 0;
inline void initing() {
	memcpy(cur, head, (t + 1) * sizeof(int));
	memset(dep, -1, sizeof(dep));
	memset(gap, 0, sizeof(gap));
}
inline void bfs() {
	int fro, ito;
	que.push(t); dep[t] = 0; ++gap[dep[t]];
	while (!que.empty()) {
		fro = que.front(); que.pop();
		for (register int i = head[fro]; ~i; i = node[i].next) {
			ito = node[i].to;
			if (dep[ito] == -1) {
				dep[ito] = dep[fro] + 1;
				que.push(ito);
				++gap[dep[ito]];
			}
		}
	}
}
ll dfs(int u, ll flow) {
	if (u == t || flow == 0)return flow; ll used = 0, wei = 0;
	for (register int i = cur[u]; ~i; i = node[i].next) {
		cur[u] = i;
		if (dep[u] == dep[node[i].to] + 1 && node[i].capa) {
			wei = dfs(node[i].to, min(flow - used, node[i].capa));
			if (wei) {
				node[i].capa -= wei;
				node[i ^ 1].capa += wei;
				used += wei;
			}
		}
		if (used == flow)return used;
	}
	--gap[dep[u]];
	if (!gap[dep[u]])dep[s] = t + 1;
	++gap[++dep[u]];
	return used;
}
ll ISAP() {
	initing(); bfs();
	while (dep[s] < t) {
		sum += dfs(s, inf);
		memcpy(cur, head, sizeof(head));
	}
	return sum;
}
ll tot[V];
inline void addE(int u, int v, ll l, ll r) {
	add(u, v, r - l);
	add(v, u, 0);
	tot[u] -= l; tot[v] += l;
}
inline void addedge(int u, int v, ll w) {
	add(u, v, w);
	add(v, u, 0);
}
inline ll solve() {
	ll judge = 0; sum = 0;
	for (int i = 1; i <= ed; i++) {
		if (tot[i] > 0)addedge(s, i, tot[i]), judge += tot[i];
		else if (tot[i] < 0)addedge(i, t, -tot[i]);
	}
	addedge(ed, st, inf); ISAP();
	ll ans = 0;
	if (sum != judge){
		sum = 0;
		return -1;
	}
	else {
		sum = 0;
		ans = node[cnt - 1].capa;
		node[cnt - 1].capa = node[cnt - 2].capa = 0;
		s = st, t = ed;
		ans += ISAP();
	}
	return ans;
}
int main() {
	ios::sync_with_stdio(0);
	cin.tie(); cout.tie();
	memset(head, -1, V * sizeof(int));
	int f, l; ll w;
	while(cin >> n >> m) {
		memset(head, -1, sizeof(head));
		memset(cur, 0, sizeof(cur));
		memset(tot, 0, sizeof(tot));
		cnt = 0;
		st = n + m + 1, ed = n + m + 2;
		s = ed + 1, t = ed + 2;  ll g;
		for (int i = 1; i <= m; i++) {
			cin >> g;
			addE(i, ed, g, inf);
		}
		int c, bh; ll d, l, r;
		for (int i = 1; i <= n; i++) {
			cin >> c >> d;
			addedge(st, i + m, d);
			for (int j = 1; j <= c; j++) {
				cin >> bh >> l >> r;
				addE(i + m, bh + 1, l, r);
			}
		}
		cout << solve() << "\n\n";
	}
	return 0;
}

有源汇上下界最小流

给定有源汇流量网络 $G$ 。询问是否存在一种标定每条边流量的方式，使得每条边流量满足上下界同时除了源点和汇点每一个点流量平衡。如果存在，询问满足标定的最小流量。

类似的，我们考虑将残量网络中不需要的流退掉。

我们找到网络上的任意一个可行流。如果找不到解就可以直接结束。

否则我们考虑删去所有附加边之后的残量网络。

我们在残量网络上再跑一次 $T$ 到 $S$ 的最大流，将可行流流量减去最大流流量即为答案。

有负圈的费用流

对于负费用边 $x\to y$ ，先让它满流，并加入边 $y\to x$ ，流量不变，费用为原费用的相反数。

此时不满足流量平衡，用类似上下界网络流的方式建附加边即可，所有附加边的费用都为 $0$ 。

#include <bits/stdc++.h>
using namespace std;
#define inf 1000000000000000
#define V 100100
#define E 200100
typedef long long int ll;
struct edge {
	int to, next;
	ll capa, cost;
};
int cnt = 0, head[V], n, m; edge node[E];
inline void add(int fir, int nxt, ll w, ll c) {
	node[cnt].to = nxt,
		node[cnt].capa = w,
		node[cnt].cost = c,
		node[cnt].next = head[fir],
		head[fir] = cnt++;
}
int s, t, cur[V]; deque<int>que; ll dep[V], sum = 0, cost = 0;
bool vis[V];
inline bool spfa() {
	for (register int i = 0; i <= n; ++i)dep[i] = inf;
	dep[s] = 0; que.push_back(s); int u, v;
	while (!que.empty()) {
		v = que.front(); que.pop_front();
		for (register int i = head[v]; i != -1; i = node[i].next) {
			u = node[i].to;
			if (dep[v] + node[i].cost < dep[u] && node[i].capa) {
				dep[u] = dep[v] + node[i].cost;
				if (!que.empty() && dep[u] < dep[que.front()])que.push_front(u);
				else que.push_back(u);
			}
		}
	}
	return (dep[t] != inf);
}
ll dfs(register int v, register ll flow) {
	if (v == t || flow == 0)return flow; ll used = 0, wei = 0;
	vis[v] = true;
	for (register int i = cur[v]; i != -1; i = node[i].next) {
		cur[v] = i;
		if (!vis[node[i].to] && dep[node[i].to] == dep[v] + node[i].cost && node[i].capa) {
			wei = dfs(node[i].to, min(flow - used, node[i].capa));
			if (wei) {
				node[i].capa -= wei,
					node[i ^ 1].capa += wei,
					used += wei,
					cost += node[i].cost * wei;
			}
		}
		if (used == flow)break;
	}
	vis[v] = false;
	return used;
}
inline void Dinic() {
	while (spfa()) {
		memcpy(cur, head, (n + 1) * sizeof(int));
		sum += dfs(s, inf);
	}
}
inline void addE(int u, int v, ll w, ll c) {
	add(u, v, w, c);
	add(v, u, 0, -c);
}
int st, ed; ll tot[V];
int main() {
	ios::sync_with_stdio(0);
	cin.tie(); cout.tie();
	memset(head, -1, V * sizeof(int));
	cin >> n >> m >> st >> ed; 
	int f, l; ll w, c;
	for (register int i = 0; i < m; ++i) {
		cin >> f >> l >> w >> c;
		if (c >= 0)addE(f, l, w, c);
		else {
			addE(l, f, w, -c);
			tot[f] -= w; tot[l] += w;
			cost += w * c;
		}
		
	}
	s = n + 1, t = n + 2; n = t;
	for (int i = 1; i <= n; i++) {
		if (!tot[i])continue;
		if (tot[i] > 0)addE(s, i, tot[i], 0);
		else addE(i, t, -tot[i], 0);
	}
	Dinic();
	s = st, t = ed; sum = 0; n -= 2;
	Dinic();
	cout << sum << " " << cost;
	return 0;
}

上下界最小费用可行流

若没有负费用边，像上下界网络流一样建图，然后跑费用流即可。(附加边的费用为 $0$ )

练习

Luogu P3980 [NOI2008] 志愿者招募

ACM

#网络流

网络流

https://je3ter.github.io/2023/08/06/ACM/网络流/

作者

Je3ter

发布于

2023年8月6日

许可协议

Codeforces Round 887 (Div. 2) 上一篇

网络流2.0 下一篇

网络流

网络流简介

网络

流

网络流的常见问题

网络流24题

最大流

概念补充

增广路

Dinic算法

前置知识

优化

代码实现

预流推进

主要思想

高度函数

推送

重贴标签

初始化

HLPP算法

过程

gap优化

代码实现

练习

最小割

概念补充

割

割的容量

最小割

最大流最小割定理

相关问题

练习

费用流

概念补充

SSP算法

代码实现

练习

上下界网络流

无源汇上下界可行流

有源汇上下界可行流

有源汇上下界最小流

有负圈的费用流

上下界最小费用可行流

练习