Manacher

Manacher 算法

简介

Manacher 算法可以 $O(n)$ 求解字符串每个位置的回文半径。

回文半径指的是从回文中心到回文串一端的字符个数。比如 abcba 的回文半径为 $3$，abba 的回文半径为 $2$。上面两个例子对应了奇回文和偶回文的情况（即回文中心落在某个字符上和回文中心落在两个字符之间）。

过程

下面介绍处理奇回文的过程，偶回文基本类似，字符串下标从 $0$ 开始。我们维护已找到的最靠右的子回文串的边界 $(l,r)$（即 $r$ 最大的回文串）。初始时，取 $l=0,r=-1$。

假设我们要对下一个 $i$ 计算回文半径 $d_i$，$d_1,d_2,\cdots,d_{i-1}$ 已经求得。我们通过以下方式计算：

• 如果 $i>r$，我们使用朴素算法，即暴力地以 $i$ 为回文中心尝试扩展回文半径。

• 如果 $i\l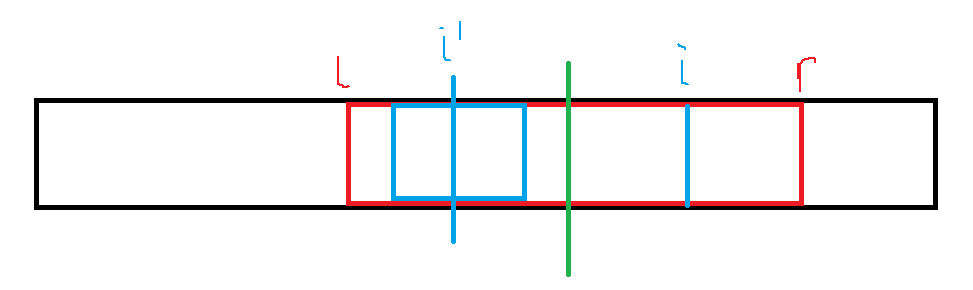eq r$，

  我们考虑 $i$ 关于当前维护的回文串的回文中心的对称点 $i'$，它的回文半径已经求出。由于 $i$ 与 $i'$ 关于回文中心对称，那么 $i$ 的回文半径显然和 $i'$ 相同。

  

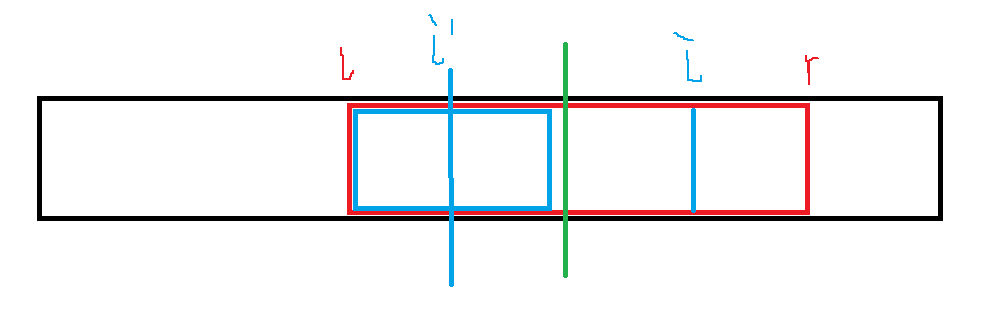
  但有一种可能的情况是，$i'$ 的回文半径恰好顶到了左端点，或者超过了左端点，此时，我们不能认为 $d_i=d_{i'}$，因为在 $[l,r]$ 以外的部分是不具有对称性的。我们先令 $d_i=r-i$，然后暴力扩展回文半径。

在计算完以后，我们更新 $[l,r]$，依此类推，直到所有点的回文半径都被计算出。

时间复杂度

由于 $r$ 单调不降，每次暴力扩展让 $r$ 增加 $1$，所以暴力扩展次数是 $O(n)$ 的，同时遍历每个点和继承对称点的回文半径也是 $O(n)$ 的。因此，总的时间复杂度是 $O(n)$ 的。

代码实现

分类讨论：

int d1[N],d2[N];//d1为奇回文中心，d偶回文中心。d2_i表示以第i个字符前一个位置为回文中心的最长回文半径
string s;cin>>s;
int n=(int)s.size();
for(int i=0,l=0,r=-1;i<n;i++)
{
	int k=(i>r?1:min(d1[l+r-i],r-i+1));
	while(i-k>=0&&i+k<n&&s[i-k]==s[i+k]) k++;
	d1[i]=k--;
	if(i+k>r) l=i-k,r=i+k;
}
for(int i=0,l=0,r=-1;i<n;i++)
{
	int k=(i>r?0:min(d2[l+r-i+1],r-i+1));
	while(i-k-1>=0&&i+k<n&&s[i-k-1]==s[i+k]) k++;
	d2[i]=k--;
	if(i+k>r) l=i-k-1,r=i+k;
}

统一处理：

可以在每个字符之间插入一个相同的占位符，这样跑一遍奇回文的情况就可以了。原来奇回文的回文串以原字符为回文中心，原来偶回文的回文串以占位符为回文中心。

int d[2*N];
string s,s0;
// 返回值为最长回文子串的长度
int Manacher()
{
    int n=2*(int)s0.size()+1;
    s.resize(n);
    for(int i=0;i<n;i++)
        if(i%2==0) s[i]='#';
        else s[i]=s0[(i-1)/2];
    for(int i=0,l=0,r=-1;i<n;i++)
    {
        int k=(i>r)?1:min(d[l+r-i],r-i+1);
        while(i-k>=0&&i+k<n&&s[i-k]==s[i+k]) k++;
        d[i]=k--;
        if(i+k>r) l=i-k,r=i+k;
    }
    int ans=0;
    for(int i=0;i<n;i++) ans=max(ans,d[i]-1);
    return ans;
}

练习

P1659 [国家集训队] 拉拉队排练

题意

给定一个字符串 $s$。令其所有奇回文子串的长度构成一个可重集 $S$，求 $S$ 的前 $k$ 大元素的乘积。结果对 $19930726$ 取模。

数据范围：$|s|\leq 10^6,k\leq 10^{12}$。

题解

简单题。若以 $i$ 为回文中心的最大回文半径为 $d_i$，显然也有回文半径为 $d_i-1,d_i-2,\cdots,1$ 。所以做一遍前缀和，然后从大到小遍历每个回文长度就可以了。

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e6+5;
const int p=19930726;
int d1[N],len[N];
ll fpow(ll a,ll b)
{
    ll res=1;
    while(b)
    {
        if(b&1) res=res*a%p;
        a=a*a%p;
        b>>=1;
    }
    return res;
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int n;ll k;cin>>n>>k;
    string s;cin>>s;
    for(int i=0,l=0,r=-1;i<n;i++)
    {
        int k=(i>r?1:min(d1[l+r-i],r-i+1));
        while(i-k>=0&&i+k<n&&s[i-k]==s[i+k]) k++;
        d1[i]=k--;
        if(i+k>r) l=i-k,r=i+k;
    } 
    for(int i=0;i<n;i++) len[2*d1[i]-1]++;
    if(n%2==0) n--;
    for(int i=n;i>2;i-=2) len[i-2]+=len[i];
    ll ans=1;
    for(int i=n;i>0;i-=2)
    {
        if(k>len[i]) 
        {
            ans=ans*fpow(i,len[i])%p;
            k-=len[i];
        }
        else
        {
            ans=ans*fpow(i,k)%p;
            k=0;
            break;
        }
    }
    if(k) cout<<-1<<'\n';
    else cout<<ans<<'\n';
    return 0;
}

P5446 [THUPC2018] 绿绿和串串

题意

定义字符串的翻转操作为以最后一个字符为对称轴进行翻转复制，例如 abcd 翻转后得到 abcdcba，qw 连续翻转两次后得到 qwqwq，z 无论进行多少次翻转操作都不会被改变。

有一个初始串 $R$，经过若干次（可能为 $0$ 次）翻转操作，得到 $R'$。现在给出 $R'$ 的前缀 $S$，求初始串 $R$ 的长度可能是多少。只需要输出不超过 $|S|$ 的 $R$ 的可能长度。

数据范围：$\sum|S|\leq 5\times 10^6$。

题解

这题比较简单。初始串 $R$ 一定是 $S$ 的前缀。倒序枚举初始串的长度 $i+1$（下标从 $0$ 开始）：

• $i\geq \dfrac{n}{2}$ 时，经过一次反转得到的长度就不小于 $S$，容易发现：长度 $i+1$ 合法当且仅当 $d_i=n-i$；
• $i\leq \dfrac{n}{2}$ 时，需要多次反转。此时，长度 $i+1$ 合法当且仅当 $d_i=i+1$ 且 $d_{2i}$ 合法。（整段前缀都可以翻转，而翻转后得到的更长的前缀已经在之前判断过了）

需要注意的是 $|S|=1$ 时长度 $1$ 是合法的。

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e6+5;
int d1[N];
bool flag[N];
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int t;cin>>t;
    while(t--)
    {
        string s;cin>>s;
        int n=(int)s.size();
        if(n==1)
        {
            cout<<1<<'\n';
            continue;
        }
        for(int i=0,l=0,r=-1;i<n;i++)
        {
            int k=(i>r?1:min(d1[l+r-i],r-i+1));
            while(i-k>=0&&i+k<n&&s[i-k]==s[i+k]) k++;
            d1[i]=k--;
            if(i+k>r) l=i-k,r=i+k;
        } 
        vector<int> ans;
        for(int i=n-1;i;i--)
        {
            if(i>=n/2) flag[i]=(d1[i]==n-i);
            else flag[i]=(d1[i]==i+1&&flag[i*2]);
            if(flag[i]) ans.push_back(i+1);
        }
        reverse(ans.begin(),ans.end());
        for(auto i:ans) cout<<i<<' ';
        cout<<'\n';
    } 
    return 0;
}