The 2022 ICPC Asia Nanjing Regional Contest

A. Stop, Yesterday Please No More

题解

首先不考虑这个洞。我们不模拟袋鼠的移动，而是模拟边界的移动，最终留下的袋鼠一定位于中间的一块矩形区域，也有可能没有袋鼠剩下，后者可以特判掉。

然后考虑这个洞。同样的，我们模拟洞的移动，看它能“吃掉“几只袋鼠。具体地，我们求出每一步洞相对于初始位置的偏移量，然后检验这些位置有多少落在了矩形区域内即可。这可以用二维前缀和实现。

代码

#include <bits/stdc++.h>
using namespace std;
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int t;cin>>t;
    while(t--)
    {
        int n,m,k;cin>>n>>m>>k;
        string s;cin>>s;
        int u=1,d=n,l=1,r=m,x=0,y=0;
        for(auto i:s)
        {
            if(i=='U') x--;
            if(i=='D') x++;
            if(i=='L') y--;
            if(i=='R') y++;
            u=max(u,1-x);
            d=min(d,n-x);
            l=max(l,1-y);
            r=min(r,m-y);
        }
        if(u>d||l>r)
        {
            if(k==0) cout<<n*m<<'\n';
            else cout<<0<<'\n';
            continue;
        }
        vector<vector<int>> sum(2*n+5);
        for(int i=0;i<2*n+5;i++) sum[i].resize(2*m+5);
        x=1,y=1;
        sum[x+n+1][y+m+1]=1;
        for(auto i:s)
        {
            if(i=='U') x++;
            if(i=='D') x--;
            if(i=='L') y++;
            if(i=='R') y--;
            sum[x+n+1][y+m+1]=1;
        }
        for(int i=1;i<=2*n+1;i++)
            for(int j=1;j<=2*m+1;j++) sum[i][j]+=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1];
        int ans=0,target=(d-u+1)*(r-l+1)-k;
        for(int i=0;i<n;i++)
            for(int j=0;j<m;j++)
            {
                int num=sum[d+n+1-i][r+m+1-j]-sum[d+n+1-i][l+m-j]-sum[u+n-i][r+m+1-j]+sum[u+n-i][l+m-j];
                if(num==target) ans++;
            }
        cout<<ans<<'\n';
    }
    return 0;
}

B. Ropeway

题解

先考虑没有修改。这是一个经典问题。设 $f_i$ 表示前 $i$ 个位置，第 $i$ 个位置选的最小代价。转移方程为

f_i=\min_jf_j+a_i

其中 $j$ 满足：

$0\leq j<i$
$i-j\leq k$
$[j+1,i-1]$ 内没有必须选的位置。

将 $n+1$ 视为代价为 $0$ 且必须选的位置，那么答案就是 $f_{n+1}$ 。利用单调队列优化可以做到 $O(n)$ 。

然后考虑修改。容易发现连续 $k$ 个位置必然有一个位置要选，所以我们可以枚举这 $k$ 个位置。只需要重新计算它们的 $f$ ，再加上以它们为起点到结尾的答案。后一部分同样可以预处理出来（预处理时可以将序列翻转，做一遍同样的dp，此时的前缀就是我们最终要求的后缀）。

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<ll,int> pli;
const int N=5e5+5;
int n,k,a[N];
ll f[N],g[N],h[N];
string s;
void solve(ll *f)
{
    f[0]=0;
    deque<int> dq;
    dq.push_front(0);
    for(int i=1;i<=n+1;i++)
    {
        while(dq.front()<i-k) dq.pop_front();
        f[i]=f[dq.front()]+a[i];
        if(i<=n&&s[i-1]=='1') dq.clear();
        while(!dq.empty()&&f[dq.back()]>=f[i]) dq.pop_back();
        dq.push_back(i);
    }
}
ll solve2(int x,int y)
{
    int old=a[x];a[x]=y;
    ll res=1e18;
    deque<pli> dq;
    for(int i=k;i>0;i--)
        if(x-i>=0)
        {
            if(s[x-i-1]=='1') dq.clear();
            while(!dq.empty()&&dq.back().first>=f[x-i]) dq.pop_back();
            dq.push_back({f[x-i],x-i});
        }
    for(int i=x;i<=x+k&&i<=n+1;i++)
    {
        while(dq.front().second<i-k) dq.pop_front();
        h[i]=dq.front().first+a[i];
        res=min(res,h[i]+g[i]);
        if(i<=n&&s[i-1]=='1') dq.clear();
        while(!dq.empty()&&dq.back().first>=h[i]) dq.pop_back();
        dq.push_back({h[i],i});
    }
    a[x]=old;
    return res;
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int t;cin>>t;
    while(t--)
    {
        cin>>n>>k;
        for(int i=1;i<=n;i++) cin>>a[i];
        a[n+1]=0;
        cin>>s;
        solve(f);
        reverse(a+1,a+n+1);
        reverse(s.begin(),s.end());
        solve(g);
        reverse(a+1,a+n+1);
        reverse(s.begin(),s.end());
        reverse(g,g+n+2);
        for(int i=1;i<=n;i++) g[i]-=a[i];
        int q;cin>>q;
        while(q--)
        {
            int x,y;cin>>x>>y;
            cout<<solve2(x,y)<<'\n';
        }        
    }
    return 0;
}

D. Chat Program

题解

考虑二分答案 $x$ ，置不小于 $x$ 的位置为 $1$ ，其余位置为 $0$ 。问题就变成了：能否通过一次操作让 $1$ 的个数不小于 $k$ 。

当添加等差数列的初始位置从左向右移动时，某位置第一次被覆盖到时，这个位置会被加上一个最大值，此后不断移动，该位置上添加的值不断减小，所以一个位置与 $x$ 的大小关系至多变化两次。我们处理出相应的位置，然后做一遍前缀和就可以了。

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=2e5+5;
int n,k,m,c,d,sum[N];
ll a[N];
bool check(ll mid)
{
    memset(sum,0,sizeof(sum));
    int cnt=0;
    for(int i=1;i<=n;i++)
        if(a[i]>=mid) cnt++;
        else
        {
            ll k=(a[i]+c>=mid?0:(d==0?1e18:(mid-a[i]-c-1)/d+1));
            if(k<=min(i-1,m-1))
            {
                sum[max(1,i-m+1)]++;
                sum[i-k+1]--;
            }
        }
    int mx=0;
    for(int i=1;i<=n;i++) sum[i]+=sum[i-1],mx=max(mx,sum[i]);
    return cnt+mx>=k;
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cin>>n>>k>>m>>c>>d;
    for(int i=1;i<=n;i++) cin>>a[i];
    ll l=0,r=1e18;
    while(l<r)
    {
        ll mid=(l+r+1)/2;
        if(check(mid)) l=mid;
        else r=mid-1;
    }
    cout<<l<<'\n';
    return 0;
}

E. Color the Tree

题解

记 $f_{i,j}$ 表示将 $i$ 子树内深度为 $j$ 的结点全部涂黑的最小代价，则

f_{u,i}=\min(a_i,\sum_{v\in son(u)}f_{v,i-1})

最终的答案就是 $\sum\limits_{i=0}^{d_1}f_{1,i}$ ，其中 $d_1$ 是从下往上的”深度“。

这是一个经典的长链剖分优化dp的形式。不过这题需要注意的是，在更新答案时，我们直接用从根到该点的所有可能选点的最小值去更新，否则长链的答案将无法被更新。

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+5;
int d[N],dep[N],mx[N];
ll dfncnt,a[N],dfn[N],*f[N],g[N];
ll st[N][20],lg[N];
vector<int> g0[N];
ll query(int x,int y)
{
    int s=lg[y-x+1];
    return min(st[x][s],st[y-(1<<s)+1][s]);
}
void dfs1(int u,int fa)
{
    d[u]=1;
    for(auto v:g0[u])
    {
        if(v!=fa)
        {
            dep[v]=dep[u]+1;
            dfs1(v,u);
            d[u]=max(d[u],d[v]+1);
            if(d[v]>d[mx[u]]) mx[u]=v;
        }   
    }
}
void dfs2(int u,int fa)
{
    dfn[u]=++dfncnt;
    f[u]=g+dfn[u];
    if(mx[u]) dfs2(mx[u],u);
    for(auto v:g0[u])
        if(v!=fa&&v!=mx[u]) dfs2(v,u);
}
void getans(int u,int fa)
{
    if(mx[u]) getans(mx[u],u);
    for(auto v:g0[u])
        if(v!=fa&&v!=mx[u])
        {
            getans(v,u);
            int len=d[v];
            for(int j=0;j<len;j++) 
            {
                f[u][j+1]+=f[v][j];
                f[u][j+1]=min(f[u][j+1],query(j+1,j+1+dep[u]));
            }
        }
    f[u][0]=query(0,dep[u]);
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int t;cin>>t;
    while(t--)
    {
        int n;cin>>n;
        dfncnt=0;
        for(int i=1;i<=n;i++) mx[i]=0,g0[i].clear();
        for(int i=0;i<n;i++) cin>>a[i];
        for(int i=2;i<=n;i++) lg[i]=lg[i>>1]+1;
        for(int i=0;i<n;i++) st[i][0]=a[i];
        for(int j=1;j<20;j++)
            for(int i=0;i+(1<<j)-1<n;i++)
                st[i][j]=min(st[i][j-1],st[i+(1<<(j-1))][j-1]);
        for(int i=1;i<n;i++)
        {
            int u,v;cin>>u>>v;
            g0[u].push_back(v),g0[v].push_back(u);
        }
        dep[1]=0;
        dfs1(1,0);
        dfs2(1,0);
        getans(1,0);
        ll ans=0;
        for(int i=0;i<d[1];i++) ans+=f[1][i];
        cout<<ans<<'\n';
    }
    return 0;
}

J. Perfect Matching

题解

当 $i-a_i=j-a_j$ 或 $i+a_i=j+a_j$ 时， $i$ 和 $j$ 有连边。我们构建这样一个二分图：每个 $i$ 可以看做是一条边，这条边连接二分图左边编号为 ( $i − a_i$ ) 的点，以及右边编号为 ( $i+a_i$ ) 的点。此时 $i$ 和 $j$ 能匹配当且仅当它们在二分图里对应的边有公共顶点。

问题转化成将一张图分解成若干条边不相交（点可以相交）的长度为 $2$ 的链。首先，对于每个连通分量，如果它含有奇数条边，那显然是无解的。否则考虑以下构造解的方式。

先随便找一棵 dfs 树，然后从深到浅考虑每一个点。找到所有和它相连的未被匹配的边，除了它连向父亲的边（这条边显然未被匹配）。如果这些边是偶数条，两两匹配即可，连向父亲的边会在处理父亲时被匹配上。如果这些边是奇数条，就把连向父亲的边也加入匹配。

这个构造方式唯一可能出问题的地方，在于根节点不存在连向父亲的边。但考虑到构造过程容易发现，当我们递归回到根节点时，此时 dfs 树上未匹配的边都是从根节点连向子节点的边（这里的子节点是直接子节点，而不是子树中的节点）。由于之前处理每个点时都让每两条边互相匹配了，如果此时未被匹配的边有奇数条，说明整个连通块边的总数也是奇数条，不符合之前的假设。因此这个构造方式一定能构造出可行解。

M. Drain the Water Tank

题解

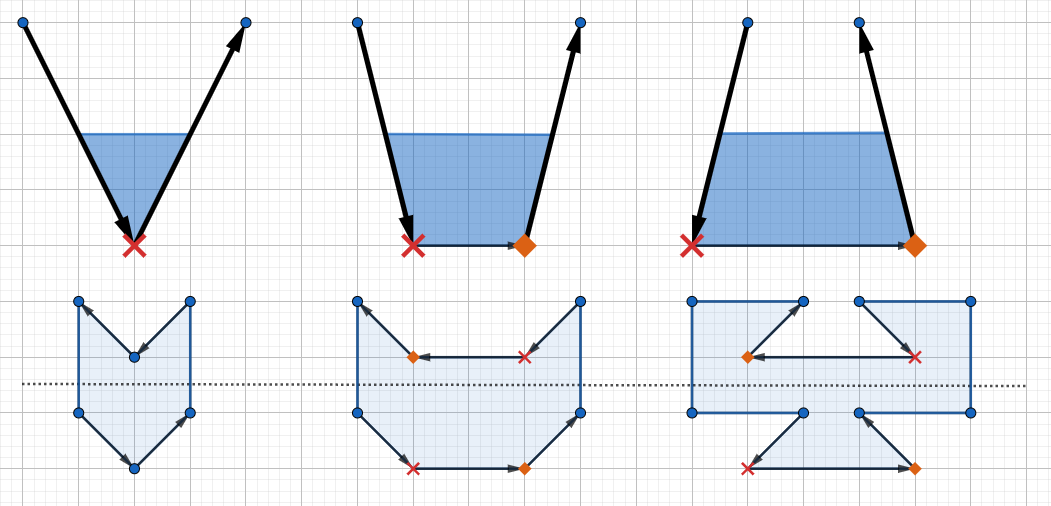
题目中要找的点就是局部最低点，局部最低点要么是一个点，要么是一条线。

当局部最低是一个点时，该点一定满足其前后两个点的 $y$ 坐标大于它。同时，为了避免误判“天花板”，需要额外判断前后两向量的叉积大于零（参考左侧的情况）。
当局部最低是一条线时，考虑以第一个点为代表，并找到线左右两侧的点。同样地，要满足 $y$ 坐标大于这条线。但此时，无法利用叉积避免误判“天花板”（参考右侧的两种情况），判断后面一个点的 $x$ 坐标大于第一个点即可。

代码

#include <bits/stdc++.h>
using namespace std;
const int N=2005;
int x[N],y[N];
int cross(int x1,int y1,int x2,int y2) {return x1*y2-x2*y1;}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int n;cin>>n;
    for(int i=0;i<n;i++) cin>>x[i]>>y[i];
    int ans=0;
    for(int i=0,j=1;i<n;i++)
    {
        while(y[j]==y[i]) j=(j+1)%n;
        int pre=(i-1+n)%n;
        if(y[i]<y[pre]&&y[i]<y[j])
        {
            if(y[i]!=y[(i+1)%n])
            {
                if(cross(x[i]-x[pre],y[i]-y[pre],x[j]-x[i],y[j]-y[i])>0) ans++;
            }
            else
            {
                if(x[(i+1)%n]>x[i]) ans++;
            }
        }
    }
    cout<<ans<<'\n';
    return 0;
}

ACM

#dp #前缀和 #2022ICPC #模拟 #二分 #计算几何 #长链剖分

The 2022 ICPC Asia Nanjing Regional Contest

https://je3ter.github.io/2023/09/26/ACM/The 2022 ICPC Asia Nanjing Regional Contest/

作者

Je3ter

发布于

2023年9月26日

许可协议

The 2022 ICPC Asia Xian Regional Contest 上一篇

AtCoder Regular Contest 165 下一篇